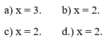tìm các số nguyên x biết 3/-4<2x/15<1/30

Những câu hỏi liên quan
bài 1 tìm các số nguyên x,y biết a)2^x=8
b) 3^4=27
c)(-1,2).x=(-1,2)^4
d)x:(-3/4)=(-3/4)^2
e)(x+1)^3=-125
f)(x-2)^3=64
bài 2 tìm các số nguyên x,y biết
a)(x-1,2)^2=4
d)(x-1,5)^2=9
e)(x-2)^3=64
a) \(2^x=8\)
⇔ \(2^x=2^3\)
⇒ \(x=3\)
b) \(3^x=27\)
⇔ \(3^x=3^3\)
⇒ \(x=3\)
c) \(\left(-\dfrac{1}{2}\right)x=\left(-\dfrac{1}{2}\right)^4\)
⇔ \(x=\left(-\dfrac{1}{2}\right)^4\div\left(-\dfrac{1}{2}\right)\)
⇔ \(x=\left(-\dfrac{1}{2}\right)^3\)
d) \(x\div\left(-\dfrac{3}{4}\right)=\left(-\dfrac{3}{4}\right)^2\)
⇔ \(x=\left(-\dfrac{3}{4}\right)^2\cdot\left(-\dfrac{3}{4}\right)\)
⇔ \(x=\left(-\dfrac{3}{4}\right)^3=-\dfrac{27}{64}\)
d) \(\left(x+1\right)^3=-125\)
⇔ \(\left(x+1\right)^3=\left(-5\right)^3\)
⇔ \(x+1=-5\)
⇔ \(x=-5-1=-6\)
Đúng 2
Bình luận (1)
2:
a: (x-1,2)^2=4
=>x-1,2=2 hoặc x-1,2=-2
=>x=3,2(loại) hoặc x=-0,8(loại)
b: (x-1,5)^2=9
=>x-1,5=3 hoặc x-1,5=-3
=>x=-1,5(loại) hoặc x=4,5(loại)
c: (x-2)^3=64
=>(x-2)^3=4^3
=>x-2=4
=>x=6(nhận)
Đúng 0
Bình luận (0)
a) tìm các số nguyên x y biết
(x-3)(xy-1)=7
b)tìm các số nguyên x y biết
y<0 và (x-3)×y=5
c)Tìm các Ư của A biết
A=1-4+5-8+9-12+...+27-30
d) tìm số nguyên x biết
(X-10)+(x-9)+(x-8)+...+(x-1)=-2015
1.Tính tổng các số nguyên x,biết :-100<x< hoặc bằng 100
2.Tìm số nguyên x+2009 là số nguyên âm lớn nhất.
3.tìm x thuộc Z,biết (x-3).(x+4)=0
1.-100<x<=100
nên xE{-99-;-98;...;99;100}
=>Tổng các số nguyên x là: -99+(-98)+...+99+100=(-99+99)+(-98+98)+...+(-1+1)+100=0+0+...+0+100=100
2.Số nguyên âm lớn nhất là: -1
nên x+2009=-1
x=-1-2009
x=-2010
3.(x-3)(x+4)=0
=>x-3=0 hoặc x+4=0
x=0+3 x=0-4
x=3 x=-4
Đúng 0
Bình luận (0)
1. Tìm x;y ∈ N* để x^4+4y^4 là số nguyên tố.2. Cho n ∈ N* CMR: n^4+4^n là hợp số với mọi n1.3. Cho biết p là số nguyên tố thỏa mãn: p^3-6 và 2p^3+5 là các số nguyên tố. CMR: p^2+10 cũng là số nguyên tố.4. Tìm tất cả các số nguyên tố có 3 chữ số sao cho nếu ta thay đổi vị trí bất kì ta vẫn thu được số nguyên tố.
Đọc tiếp
1. Tìm x;y ∈ N* để \(x^4+4y^4\) là số nguyên tố.
2. Cho n ∈ N* CMR: \(n^4+4^n\) là hợp số với mọi n>1.
3. Cho biết p là số nguyên tố thỏa mãn: \(p^3-6\) và \(2p^3+5\) là các số nguyên tố. CMR: \(p^2+10\) cũng là số nguyên tố.
4. Tìm tất cả các số nguyên tố có 3 chữ số sao cho nếu ta thay đổi vị trí bất kì ta vẫn thu được số nguyên tố.
1.
\(x^4+4y^4=x^4+4x^2y^2+y^4-4x^2y^2=\left(x^2+2y^2\right)^2-\left(2xy\right)^2\)
\(=\left(x^2-2xy+2y^2\right)\left(x^2+2xy+2y^2\right)\)
Do x, y nguyên dương nên số đã cho là SNT khi:
\(x^2-2xy+2y^2=1\Rightarrow\left(x-y\right)^2+y^2=1\)
\(y\in Z^+\Rightarrow y\ge1\Rightarrow\left(x-y\right)^2+y^2\ge1\)
Đẳng thức xảy ra khi và chỉ khi \(x=y=1\)
Thay vào kiểm tra thấy thỏa mãn
2. \(N=n^4+4^n\)
- Với n chẵn hiển nhiên N là hợp số
- Với \(n\) lẻ: \(\Rightarrow n=2k+1\)
\(N=n^4+4^n=n^4+4^{2k+1}=n^4+4.4^{2k}+4n^2.4^k-n^2.4^{k+1}\)
\(=\left(n^2+2.4^k\right)^2-\left(n.2^{k+1}\right)^2=\left(n^2+2.4^k-n.2^{k+1}\right)\left(n^2+2.4^k+n.2^{k+1}\right)\)
Mặt khác:
\(n^2+2.4^k-n.2^{k+1}\ge2\sqrt{2n^2.4^k}-n.2^{k+1}=2\sqrt{2}n.2^k-n.2^{k+1}\)
\(=n.2^{k+1}\left(\sqrt{2}-1\right)\ge2\left(\sqrt{2}-1\right)>1\)
\(\Rightarrow N\) là tích của 2 số dương lớn hơn 1
\(\Rightarrow\) N là hợp số
Đúng 1
Bình luận (0)
Bài 4 chắc không có cách "đại số" nào (tức là dựa vào lý luận chia hết tổng quát) để giải. Mình nghĩ vậy (có lẽ có, nhưng mình ko biết).
Chắc chỉ sáng lọc và loại trừ theo quy tắc kiểu: do đổi vị trí bất kì đều là SNT nên không thể chứa các chữ số chẵn và chữ số 5, như vậy số đó chỉ có thể chứa các chữ số 1,3,7,9
Nó cũng không thể chỉ chứa các chữ số 3 và 9 (sẽ chia hết cho 3)
Từ đó sàng lọc được các số: 113 (và các số đổi vị trí), 337 (và các số đổi vị trí)
Đúng 1
Bình luận (9)
Tìm x nguyên biết các phân số sau là số nguyên : a)26/x+3 ;x-2/x+3 ;x+6/x+3 ;15/x-4
a;26/x+3 la so nguyen nen 2 6 chia het cho x+3
dan den x+3 thuoc uoc cua 26
ma uoc cua 26 la 1;-1;2;-2;13;-13;26;-26
khi x+3=1 thi x=-2 khi x+3=13 thi x= 10
khi x+3=-1 thi x=-4 khi x+3=-13 thi x=-16
khi x+3=2 thi x=-1 khi x+3=26 thi x= 23
khi x+3=-2 thi x=-5 khi x+3=-26 thi x= -29
x-2/x+3 la so nguyen nghia la x-2 chia het cho x+3
x-2 =x+3-5 chia het cho x+3
suy ra 5 chia het cho x+3
ma uoc cua 5 la -5;-1;5;1
khi x+3=-5thi x=-8 khi x+3 =5 thi x=2
khi x+3=-1 thi x=-4 khi x+3=1 thi x=-2
x+6/x+3 la so nguyen nen x+6 chia het cho x+3
ta co x+6 =x+3+3 chia het cho x+3
suy ra 3 chia het cho x+3
ma uoc cua x+3 la 3;1;-1;-3
khi x+3=3thi x=0 khi x+3=-3 thi x=-6
khi x+3=1 thi x=-2 khi x+3 = -1 thi x=-4
15/x-4 la so nguyen nen 15 chia het cho x-4
ma uoc cua 15 la 1;3;5;15;-1;-3;-5;-15
khi x-4=1 thi x=5 khi x-4=-1 thi x=3
khi x-4 =3 thi x=7 khi x-4 =-3 thi x=1
khi x-4=5 thi x=9 khi x-4 =-5 thi x =-1
khi x-4=15 thi x=19 khi x-4=-15 thi x=-11
Đúng 0
Bình luận (0)
Tìm tổng tất cả các số nguyên x biết: -4 < x < 3
Các số nguyên nằm giữa –4 và 3 là –3; –2; –1; 0; 1; 2.
Vậy x ∈ {–3; –2; –1; 0; 1; 2}.
+ Tính tổng các số nguyên x:
(–3) + (–2) + (–1) + 0 + 1 + 2 = (–3) + [(–2) + 2] + [(–1) + 1] + 0
= (–3) + 0 + 0 + 0 = –3
Đúng 0
Bình luận (0)
Tìm các số nguyên x, biết: a) (- 4). x = -12 b) ( - 17). x = -34 c) 4 . x - 3 = 5 d) ( -4) . x +3 = -5
tìm các số nguyên x,y biết
x-4/y-3=4/3 và x-y=5
Tìm các cặp số nguyên x, y biết:
\(\dfrac{5}{x}-\dfrac{4}{3}=x\)
Tìm các số nguyên x;y biết rằng: (x - 2)^2 . (y-3) = -4
\(\left(x-2\right)^2.\left(y-3\right)=-4\\ \rightarrow\left(x-2\right)^2\inƯ\left(4\right),y-3\inƯ\left(4\right).\)
Vì x, y nguyên. Do đó \(\left(x-2\right)^2=1\) hoặc \(\left(x-2\right)^2=4.\)
TH1: \(\left(x-2\right)^2=1\) suy ra x = 1 hoặc x = 3
Khi đó y - 3 = 4 suy ra y = 7.
TH2: \(\left(x-2\right)^2=4\) suy ra x = 4 hoặc x = 0.
Khi đó y - 3 = 1 suy ra y = 4.
Vậy có 4 cặp x, y thỏa mãn là (x, y) = (1, 7); (3, 7); (4, 4); (0, 4)
Đúng 3
Bình luận (0)
Lời giải:
Với $x,y$ nguyên thì $(x-2)^2, y-3$ cũng nguyên và $(x-2)^2$ số chính phương nên không âm.
Tích 2 số nguyên bằng $-4$ nên xảy ra các TH sau:
TH1: $(x-2)^2=1; y-3=-4$
$\Rightarrow x=1$ hoặc $x=3; y=-1$. Ta có $(x,y)=(1,-1); (3,-1)$
TH2: $(x-2)^2=4; y-3=-1$
$\Rightarrow x=0$ hoặc $x=4; y=2$. Ta có $(x,y)=(0,2); (4,2)$
Đúng 3
Bình luận (0)