Cho đường tròn (o) và hai dây MA,MB vuông góc với nhau. Gọi I và K lần lượt là điểm chính giữa của các cung nhỏ MA và MB. Gọi P là giao điểm của AK và BI.
a. Chứng minh rằng ba điểm A, O, B thẳng hàng.
b. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác MAB
c. Giả sử MA=12; MB=16, tính bán kính của đường tròn nội tiếp tam giác MAB.

Những câu hỏi liên quan
Cho đường tròn (O) và 2 dây MA, MB vuông góc với nhau. Gọi I và K lần lượt là điểm chính giữa của các cung nhỏ MA và MB. Gọi P là giao điểm AK và BI.
a) Chứng minh rằng: 3 điểm A, O, B thẳng hàng?
b) Chứng minh rằng: P là tâm đường tròn nội tiếp MAB?
c) Giả sử MA=12cm; MB=16cm. Tính bán kính của đường tròn nội tiếp MAB?
Cho đường tròn (O) và hai dây MA, MB vuông góc với nhau. Gọi I, K lần lượt là điểm chính giữa của các cung nhỏ MA và MB
a, Chứng minh ba điểm A, O, B thẳng hàng
b, Gọi P là giao điểm của AK và BI. Chứng minh P là tâm đưòng tròn nội tiếp tam giác MAS
a, Chú ý: M,A,B(O) và A M B ^ = 90 0 => ĐPCM
b, Gợi ý: Chứng minh AK và BI lần lượt là phân giác trong góc A, B của tam giác MAB
Đúng 1
Bình luận (0)
Cho (O) và 2 dây MA, MB vuông góc với nhau. Gọi I,K lần lượt là điểm chính giữa của các cung nhỏ MA và MB
a, Chứng minh A,O,B thẳng hàng
b, Gọi P là giao điểm của AK và BI. Chứng minh P là tâm đường tròn nội tiếp tam giác MAB
Answer:
a, \(\Delta MAB\) nội tiếp \(\left(O\right)\) có \(\widehat{AMB}=90^o\)
\(\Rightarrow AB\) là đường kính \(\left(O\right)\)
\(\Rightarrow AB\) đi qia tâm O của đường tròn
Vậy ba điểm A, O, B thẳng hàng
b, Vì I là điểm chính giữa cung nhỏ MA
\(\Rightarrow\widebat{IA}=\widebat{IM}\)
\(\Rightarrow\widehat{ABI}=\widehat{MBI}\)
\(\Rightarrow IB\) là tia phân giác của \(\widehat{MBA}\)
Vì K là điểm chính giữa cung nhỏ MB
\(\Rightarrow\widebat{KB}=\widebat{KM}\)
\(\Rightarrow\widehat{BAK}=\widehat{MAK}\)
\(\Rightarrow AK\) là tia phân giác của \(\widehat{MAK}\)
\(\Delta MAB\) có hai đường phân giác AK và IB cắt nhau tại P
Vậy P là đường tròn nội tiếp \(\Delta MAB\)
cho đường tròn (O) và hai dây MA,MB vuông góc với nhau. gọi I,K lần lwojt là điểm chính giữa của các cung nhỏ MA và MB.
a) C/M 3 điểm A,O,B thẳng hàng
b) gọi P là giao điểm của AK và BI. C/M P là tâm đường tròn nội tiếp tam giác MAB.
Cho (O) và hai dây MA và MB vuông góc với nhau. Gọi I và K lần lượt là điểm chính giữa của cung nhỏ MA và MB. Gọi P là giao của AK và BI.
a) A,O,B thẳng hàng
b) P là tâm đường tròn nội tiếp tam giác MAB.
c*) giả sử: MA= 12cm, MB= 16cm. Tính bán kính đường tròn nội tiếp tam giác MAB.
b, sửa đề AI giao BK = P
Góc MAI = BAI ( = 1/2 sđ cung MI ; cùng đường tròn tâm O ) => AI là tia phân giác MAI
tt BK là phân giác MBA
=> giao P .............đpcm
c, Ta có định lý : 2 x \(S\)MAB = MB x MA = ( MA + MB + AB ) x r
r là bán kính đường tròn nội típ
Thay số tính típ
Đúng 0
Bình luận (0)
Cho đường tròn (O) và 2 dây MA,MB vuông góc với nhau. Gọi I,K lần lượt là điểm chính giữa của các cung nhỏ MA và MB. Gọi P là giao điểm của AK và BI
a) Cmr 3 điểm A,O,B thẳng hàng
b) Cmr P là tâm đường tròn nội tiếp tam
giacs MAB
c) Giả sử MA=12cm, MB=16cm, tính bán kính của đường tròn nội tiếp tam giác MAB
Bài 4: Từ một điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB, MA, MB. Gọi I là giao điểm AC và DE, K là giao điểm của BC và DF.
Chứng minh rằng :
a) Các tứ giác AECD, BFCD nội tiếp.
b) CD^2 =CE.CF.
c) Tứ giác ICKD nội tiếp được đường tròn.
d) IK _|_ CD
Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB, MA, MB. Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng: IK ⊥ CD
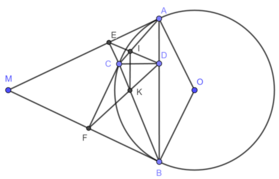

( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC)

Đúng 0
Bình luận (1)
Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB, MA, MB. Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng: C D 2 = CE.CF
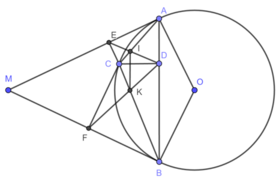

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC) (2)

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CB) (5)

Đúng 1
Bình luận (0)


















