giải và biện luận cho phương trình sau
(m + 2)x + 4(2m + 1) = m^2 + 4(x - 1)
Giải và biện luận phương trình sau:
a)m/2m-x=2
b)x+1+1/x-1=m(x-3)
c)(x²+(m+2)x-m)/x+1=-x-4
Bài 1: Giải các bất phương trình:
3(1 - x)> \(\dfrac{7-3x^2}{x+1}\)
Bài 2. Giải và biện luận bất phương trình
( m2 - 4 ) x +3 > ( 2m -1) x +m
Giải và biện luận các phương trình sau theo tham số m: (2m + 1)x - 2m = 3x - 2
(2m + 1)x – 2m = 3x – 2
⇔ (2m + 1)x – 3x = 2m – 2
⇔ (2m + 1 – 3).x = 2m – 2
⇔ (2m – 2).x = 2m – 2 (3)
+ Xét 2m – 2 ≠ 0 ⇔ m ≠ 1, pt (3) có nghiệm duy nhất 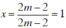
+ Xét 2m – 2 = 0 ⇔ m = 1, pt (3) ⇔ 0.x = 0, phương trình có vô số nghiệm.
Kết luận :
+ Với m = 1, phương trình có vô số nghiệm
+ Với m ≠ 1, phương trình có nghiệm duy nhất x = 1.
Bài 1: Giải và biện luận các phương trình sau:
a) m(m-x)= 3(x+3)-6m
b) mx-3m=2x-3
c) (m^2 -9)x=m^2 +3m
Bài 2: Giải và biện luận các phương trình sau:
a) m(m-1)=2(2x+1)
b) (m^2 - 9)x=m^2 +3m
c) m(m-1)= 2(4-x)
d) (m^2 -3m+2)x= m-2
Các cậu giúp tớ với ạ, không cần làm hết đâu ạ, mng biết câu nào thì làm hộ tớ với nhé, plss!
Vì hai bài giống nhau nên anh sẽ làm mẫu bài 1 nhé.

Giải và biện luận theo tham số m các phương trình sau
m x 2 + ( 2 m - 1 ) x + m - 2 = 0
m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là
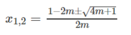
Giải và biện luận hệ phương trình:
Từ (1) y = mx – 2m, thay vào (2) ta được:
4x – m(mx – 2m) = m + 6 (m2 – 4)x = (2m + 3)(m – 2) (3)
+ Nếu m2 – 4 0 hay m
2 thì x =
Khi đó y = - . Hệ có nghiệm duy nhất: (
;-
)
+ Nếu m = 2 thì (3) thỏa mãn với mọi x, khi đó y = mx -2m = 2x – 4
Hệ có vô số nghiệm (x, 2x-4) với mọi x thuộc R
+ Nếu m = -2 thì (3) trở thành 0x = 4 . Hệ vô nghiệm
mọi người giải thích giúp mình phần tô đậm nhé
Giải và biện luận hệ phương trình \(\begin{cases} 4x-my=m-4 \\ (2m+6)x+y=2m+1 \end{cases} \)
\(\left\{{}\begin{matrix}4x-my=m-4\\\left(2m+6\right)x+y=2m+1\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{4}{2m+6}< >\dfrac{-m}{1}\)
=>\(-2m^2-6m< >4\)
=>\(-2m^2-6m-4\ne0\)
=>\(-2\left(m^2+3m+2\right)\ne0\)
=>\(m^2+3m+2\ne0\)
=>\(\left(m+1\right)\left(m+2\right)\ne0\)
=>\(\left\{{}\begin{matrix}m+1\ne0\\m+2\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne-1\\m\ne-2\end{matrix}\right.\)
=>\(m\notin\left\{-1;-2\right\}\)
Để hệ phương trình vô nghiệm thì \(\dfrac{4}{2m+6}=\dfrac{-m}{1}\ne\dfrac{m-4}{2m+1}\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{2m+6}=-m\\\dfrac{-m}{1}\ne\dfrac{m-4}{2m+1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2m^2-6m=4\\-2m^2-m\ne m-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2m^2-6m-4=0\\-2m^2-2m+4\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2+3m+2=0\\m^2+m-2\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(m+1\right)\left(m+2\right)=0\\\left(m+2\right)\left(m-1\right)\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m+1=0\\m+2=0\end{matrix}\right.\\\left\{{}\begin{matrix}m+2\ne0\\m-1\ne0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\in\left\{-1;-2\right\}\\m\notin\left\{-2;1\right\}\end{matrix}\right.\Leftrightarrow m=-1\)
Để hệ phương trình có vô số nghiệm thì \(\dfrac{4}{2m+6}=\dfrac{-m}{1}=\dfrac{m-4}{2m+1}\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{2m+6}=-m\\\dfrac{m-4}{2m+1}=-m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-m=\dfrac{2}{m+3}\\m-4=-m\left(2m+1\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-m^2-3m=2\\m-4+2m^2+m=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+3m=-2\\2m^2+2m-4=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2+3m+2=0\\m^2+m-2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(m+2\right)\left(m+1\right)=0\\\left(m+2\right)\left(m-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\in\left\{-2;-1\right\}\\m\in\left\{-2;1\right\}\end{matrix}\right.\)
=>m=-2
giải và biện luận phương trình sau:
a, m(x-1)=5-(m-1)x
b, (m*m-2m)x+5=5m-mx
với m là tham số (m*m là m mũ 2)
Giải và biện luận phương trình sau theo tham số m:
\(\dfrac{ 2m-1 }{ x-1 } = m-2\)
mình đg cần gấp, giúp mình nhé
x= 3m-3/m-2
Tại m =2 thì pt vô nghiệm
Tại m khác 2 thì có nghiệm duy nhất vì đây là hàm bậc nhất