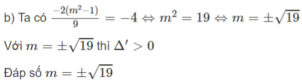Phương trình(x+4)(9x2−1)=0 có các nghiệm là?

Những câu hỏi liên quan
Trong các phương trình sau,phương trình nào có ít nhất một nghiệm là số nguyên?
A.\(\left(x-\sqrt{5}\right)^2=5\) B.9x2-1=0 C.4x2-4x+1=0 D.x2+x+2=0
Phương trình
9
x
2
+
x
−
1
−
10.3
x
2
+
x
−
2
+
1
0
có tập nghiệm là: A.
−
2...
Đọc tiếp
Phương trình 9 x 2 + x − 1 − 10.3 x 2 + x − 2 + 1 = 0 có tập nghiệm là:
A. − 2 ; − 1 ; 1 ; 2
B. − 2 ; 0 ; 1 ; 2
C. − 2 ; − 1 ; 0 ; 1
D. − 1 ; 0 ; 2
Đáp án C
Ta có P T ⇔ 9 x 2 + x + 1 − 10 3 .3 x 2 + x + 1 = 0
Đặt t = 3 x 2 + x + 1 ⇒ t 2 − 10 3 t + 1 = 0
⇔ t = 3 t = 1 3 ⇒ x 2 + x + 1 = 1 x 2 + x + 1 = − 1 ⇔ x = 1 ; x = − 2 x = 0 ; x = − 1
Đúng 0
Bình luận (0)
Cho phương trình
9
x
2
+
2
(
m
2
-
1
)
x
+
1
0
.Xác định m để phương trình có hai nghiệm
x
1
,
x
2
m
à
x...
Đọc tiếp
Cho phương trình 9 x 2 + 2 ( m 2 - 1 ) x + 1 = 0 .Xác định m để phương trình có hai nghiệm x 1 , x 2 m à x 1 + x 2 = - 4
Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:
a
)
4
x
2
+
2
x
−
5
0
b
)
9
x
2...
Đọc tiếp
Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:
a ) 4 x 2 + 2 x − 5 = 0 b ) 9 x 2 − 12 x + 4 = 0 c ) 5 x 2 + x + 2 = 0 d ) 159 x 2 − 2 x − 1 = 0
a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: 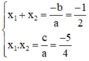
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: 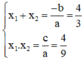
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: 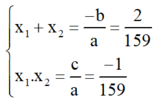
Đúng 0
Bình luận (0)
Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:
9x2 – 12x + 4 = 0
Phương trình 9x2 – 12x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ’ = (-6)2 – 4.9 = 0
⇒ Phương trình có nghiệm kép x1 = x2.
Theo hệ thức Vi-et ta có: 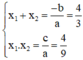
Đúng 0
Bình luận (0)
Cho phương trình 9 x 2 + 2 ( m 2 - 1 ) x + 1 = 0 . Chứng tỏ rằng với m > 2 phương trình có hai nghiệm phân biệt âm.
Tìm các giá trị của k sao cho phương trình : 9x2–32+k2–2k.x = 0 có nghiệm x =2
9x^2 - 32 + k^2 - 2k.x = 0
Thay x = 2 vào, ta có:
<=> 9.2^2 - 32 + k^2 - 2k.2 = 0
<=> 36 - 32 + k^2 - 4k = 0
<=> 4 + k^2 - 4k = 0
<=> (2 - k)^2 = 0
<=> 2 - k = 0
<=> k = 2
cho phương trình :
x^2 - 10mx + 9m = 0
tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thõa : x1 - 9x2 = 0
Để phương trình có hai nghiệm phân biệt thì:
\(\left(-10m\right)^2-36m>0\Leftrightarrow100m^2-36m>0\Leftrightarrow m\left(100m-36>0\right)\)
\(\Leftrightarrow m>0,36\)
Giải phương trình :
x2 - 10mx + 9m = 0
\(\Delta=0,36\Rightarrow\sqrt{\Delta}=0,6\)
<=> x1 = 5m - 0,3
x2 = 5m + 0,3
x1 - 9x2 = 0
ok , lm tiếp đi
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số thực m để phương trình sau có đúng 3 nghiệm thực phân biệt
9
x
2
-
2
.
3
x
2
+
1
+
3
m
-
1
0
A. m
10
3
B. 2 m
10
3
C. m 2 D. m 2
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để phương trình sau có đúng 3 nghiệm thực phân biệt 9 x 2 - 2 . 3 x 2 + 1 + 3 m - 1 = 0
A. m = 10 3
B. 2 < m < 10 3
C. m = 2
D. m < 2