Cho \(\Delta ABC\)vuông tại A. Biết 3AB = 4AC và BC = 20cm. Tính độ dài các cạnh AC

Những câu hỏi liên quan
cho tam giác abc vuông tại a, biết 3ab = 4ac và bc = 20cm. tính đọ dài các cạnh ab, ac
Cho tam giác ABC vuông tại A. Biết 3AB=4AC và BC=20 cm. Tính độ dài các cạnh AB và AC
Cho tam giác ABC vuông tại A.Biết 3AB=4AC và BC=20cm .Tính độ dài các cạnh AB và AC
Cho tam giác ABC vuông tại A . Biết 3AB = 4AC và Bc = 25 cm . Tình độ dài các cạnh AB, AC.
Mọi người giải giùm mình nha!
Thứ 6 là mình phải làm rồi!
Ta có \(\dfrac{AB}{4}=\dfrac{AC}{3}\Rightarrow\dfrac{AB^2}{16}=\dfrac{AC^2}{9}\)
Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{AB^2}{16}=\dfrac{AC^2}{9}=\dfrac{BC^2}{25}=\dfrac{25^2}{25}=25\Rightarrow AB=20cm;AC=15cm\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Biết 3AB=4AC và AB-AC=2cm.Tính độ dài các cạnh AB,AC
bai toan dang hieu va ty cua lop 4 do bạn;
ab/ac = 3/4
ab-ac =2
ab =6
ac=8
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Biết 3AB=4AC và AB-AC=2cm.Tính độ dài các cạnh AB,AC
Cho \(\Delta\)ABC vuông ở A biết BC=20cm và 4.AB=3.AC.Tính độ dài các cạnh AB,AC
Ta có: \(\Delta\)ABC vuông tại A => \(AB^2+AC^2=BC^2=400\)
Ta có: \(\frac{AB}{3}=\frac{AC}{4}\Leftrightarrow\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{9+16}=\frac{400}{25}=16\)
\(\Rightarrow\hept{\begin{cases}AB^2=16.9=144\\AC^2=16^2\end{cases}}\)=> AB=12 và AC=16
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A,biết ab=4ac và bc=20cm.Tính độ dài các cạnh AB và AC
Cho tam giác ABC vuông tại A và đường cao AH. Biết A = 90 độ, AB = 15cm, AC = 20cm.
a) TÍnh cạnh BC.
b) Tính độ dài của AH, BH và HC
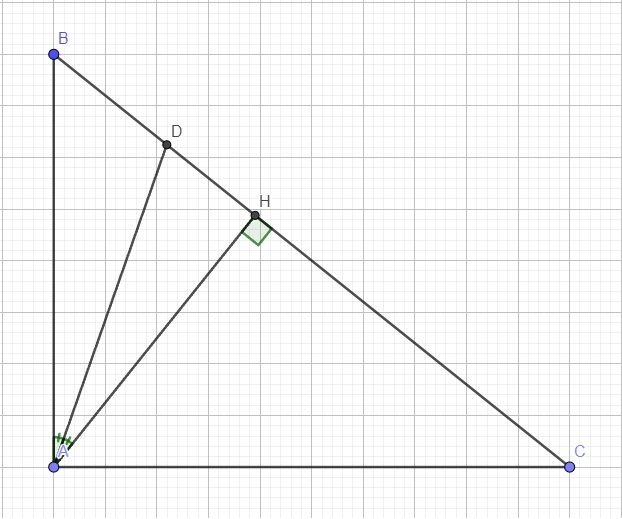
Câu hỏi: Cho ∆ABC vuông tại A có AB15cm, AC20cm. Vẽ AH vuông góc với BC tại H.a) Chứng minh ∆HBA đồng dạng với ∆ABCb) Tính độ dài các cạnh BC, HAc) Vẽ tia phân giác của góc BAH cắt BH tại D. Tính độ dài các cạnh DB, DH
Đọc tiếp
Câu hỏi: Cho ∆ABC vuông tại A có AB=15cm, AC=20cm. Vẽ AH vuông góc với BC tại H.
a) Chứng minh ∆HBA đồng dạng với ∆ABC
b) Tính độ dài các cạnh BC, HA
c) Vẽ tia phân giác của góc BAH cắt BH tại D. Tính độ dài các cạnh DB, DH
a.
Xét hai tam giác HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{B}\text{ chung}\\\widehat{BHA}=\widehat{BAC}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
b.
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Từ câu a ta có: \(\dfrac{HA}{AC}=\dfrac{BA}{BC}\Rightarrow HA=\dfrac{AB.AC}{BC}=12\left(cm\right)\)
c.
Áp dụng định lý Pitago cho tam giác vuông HBA:
\(BH=\sqrt{AB^2-HA^2}=9\left(cm\right)\)
Do AD là phân giác, áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DH}{AH}\Rightarrow\dfrac{BD}{AB}=\dfrac{BH-BD}{AH}\)
\(\Rightarrow12BD=15\left(9-BD\right)\Rightarrow BD=5\left(cm\right)\)
\(\Rightarrow DH=BH-BD=4\left(cm\right)\)
Đúng 1
Bình luận (0)