cho đường tròn tam O với M bên ngoài kẻ tiếp tuyến MA và MB đường kính AC cua O chung minh OM//BC

Những câu hỏi liên quan
Cho đường tròn(O; R), điểm M nằm phía bên ngoài đường tròn sao cho OM = 2R. Từ điểm M kẻ các tiếp tuyến MB, MC với đường tròn (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OM và BC. a) Chứng minh: OM ⊥ BC tại H. b) Kẻ đường kính BD, chứng minh: CD//OM c) Tính MH.MO theo R. Tính 𝐵𝑀𝐶 = ? d) MD cắt đường tròn (O) tại điểm thứ hai là E. Chứng minh: MH.MO = ME.MD
cho đường tròn (O,R), điểm M nằm bên ngoài đường tròn. Kẻ các tiếp tuyến MA, MB ứng với đường tròn (A, B là các tiếp điểm)
a, CM OM vuông góc AB
b, vẽ đường kính AC. CM OM song song BC
cho đường tròn tâm o bán kính và m là một điểm nằm bên ngoài đường tròn . từ m kẻ hai tiếp tuyến từ ma,mb với đường tròn r (o) (a b là các tiếp điểm gọi e là giao điểm của ab và om
cho đường tròn tâm o bán kính và m là một điểm nằm bên ngoài đường tròn . từ m kẻ hai tiếp tuyến từ ma,mb với đường tròn r (o) (a b là các tiếp điểm gọi e là giao điểm của ab và om
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn(O) với A,B là các tiếp điểm.
a) Cm 4 điểm A,B,M,O cùng thuộc 1 đường tròn
b) Kẻ đường kính AC của đường tròn (O). Cm: OM//CB
c) Vẽ BK vuống góc với AC tại K. Chứng minh CK.OM=OB.CB
d) Tiếp tuyến tại C của đường tròn(O) cắt AB tại D. Cm OD vuống góc với CM
Cho (O) và một điểm M nằm ngoài đường tròn.Từ M kẻ hai tiếp tuyến MA và MB với đường tròn (O).Gọi I là giao của OM và AB,kẻ đường kính BC của (O)
a)Chứng minh OI.OM=OA2
b)Qua O vẽ đường thẳng vuông góc với MC tại E cắt BA tại F.Chứng minh FC là tiếp tuyến của (O)
a: Xét (O) có
MA,MB là tiếp tuyến
nên MA=MB
mà OA=OB
nên OM là trung trực của AB
Xét ΔOAM vuông tại A có AI là đường cao
nên OI*OM=OA^2=R^2
b: Xét ΔOIF vuông tại I và ΔOEM vuông tại E có
góc IÒ chung
Do đó: ΔOIF đồng dạng với ΔOEM
=>OI/OE=OF/OM
=>OE*OF=OI*OM=OA^2=OC^2=R^2
=>FC là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .
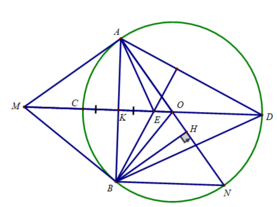
c) Ta có: ∠(ABN ) = 90 0 (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) = 90 0
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
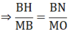
Hay MB. BN = BH. MO
Đúng 1
Bình luận (0)
cho đường tròn tâm o. từ điểm m nằm ngoài đường tròn tâm o kẻ tiếp tuyến ma của đường tròn tâm o. từ a kẻ đường thẳng vuông góc với om cắt om và đường tron tâm o lần lượt tại h và b. chứng minh bm là tiếp tuyến đường tròn tâm o. kẻ đường kính ac, mc cắt đường tròn tâm o tại d, kẻ di vuông góc với ac, di cắt ab tại g ,gọi e là trung điểm am, chứng minh c f e thẳng hàng
a: ΔOAB cân tại O
mà OM là đường cao
nên OM là phân giác
Xét ΔOAM và ΔOBM có
OA=OB
góc AOM=góc BOM
OM chung
=>ΔOAM=ΔOBM
=>góc OBM=90 độ
=>MB là tiếp tuyến của (O)
b:F ở đâu vậy bạn?
Đúng 0
Bình luận (3)
Bài 7 (3 điểm). Từ điểm M ở ngoài đường tròn (O; R), vẽ hai tiếp tuyến MA, MB với đường tròn (0) (A, B là 2 tiếp điểm). OM cắt AB tại H. Vẽ đường kính BC của đường tròn (O).
a) Chứng minh OM 1 AB và AC // MO.
b) Chứng minh OH. OM = R2 và OCH = OMC













