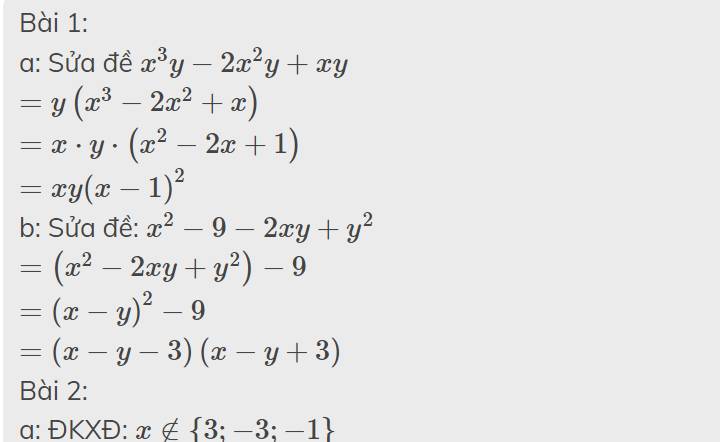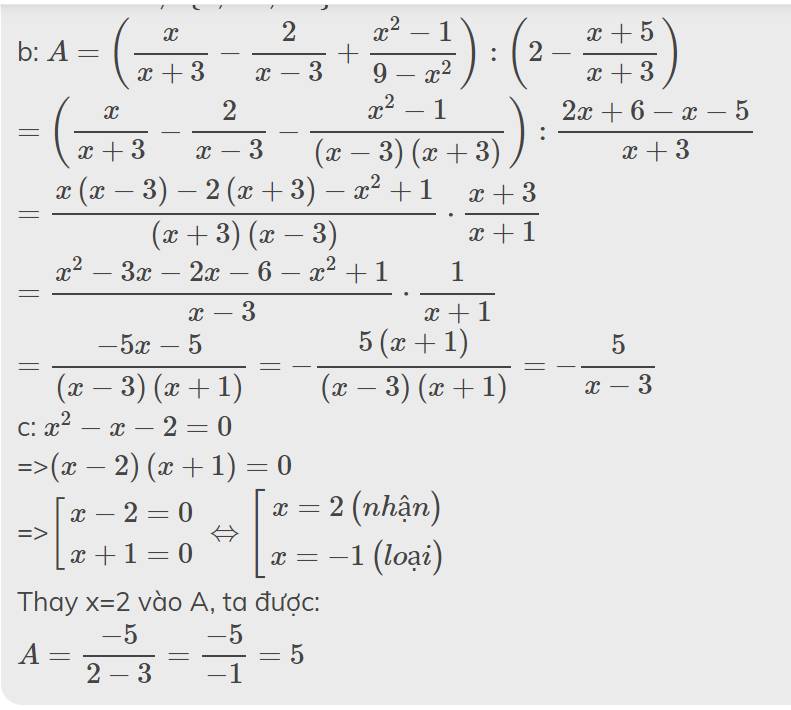rút gọn bt {[1/(x^2+2xy+y^2)]-[1/(x^2-y^2)]}/(4xy/y^2-x^2)

Những câu hỏi liên quan
Rút gọn A=[ 1/(x2 + 2xy+ y2)-1/(x2-y2)] : 4xy/ (y2-x2)
\(A=\left(\frac{1}{x^2+2xy+y^2}-\frac{1}{x^2-y^2}\right):\frac{4xy}{y^2-x^2}\)ĐK : \(x\ne y;x\ne-y;x;y\ne0\)
\(=\left(\frac{x-y}{\left(x-y\right)\left(x+y\right)^2}-\frac{x+y}{\left(x-y\right)\left(x+y\right)^2}\right):\frac{4xy}{y^2-x^2}\)
\(=\frac{2y}{\left(x-y\right)\left(x+y\right)^2}.\frac{\left(x-y\right)\left(x+y\right)}{4xy}=\frac{1}{2x\left(x+1\right)}\)
Rút gọn \(\left(\frac{1}{x^2+2xy+y^2}-\frac{1}{x^2-y^2}\right):\frac{4xy}{y^2-x^2}\)
ĐKXĐ: x2-y2\(\ne\)0 4xy\(\ne\)0
\(\Leftrightarrow\)\(\left(x-y\right)\left(x+y\right)\ne0\) <=>x\(\ne\)0 và y \(\ne\)0
\(\Leftrightarrow x\ne y\) và \(x\ne-y\)
Đặt P= \(\left(\frac{1}{x^2+2xy+y^2}-\frac{1}{x^2-y^2}\right):\frac{4xy}{y^2-x^2}\)
<=>\(\left(\frac{1}{\left(x+y\right)^2}-\frac{1}{\left(x+y\right)\left(x-y\right)}\right).\frac{y^2-x^2}{4xy}\)
<=>\(\left(\frac{x-y}{\left(x+y\right)^2\left(x-y\right)}-\frac{x+y}{\left(x+y\right)^2\left(x-y\right)}\right).\frac{-\left(x^2-y^2\right)}{4xy}\)
<=>\(\frac{x-y-x-y}{\left(x+y\right)^2\left(x-y\right)}.\frac{-\left(x-y\right)\left(x+y\right)}{4xy}=\frac{-2y}{\left(x+y\right)^2\left(x-y\right)}.\frac{-\left(x-y\right)\left(x+y\right)}{4xy}\)
<=>\(\frac{1}{2x\left(x+y\right)}=\frac{1}{2x^2+2xy}\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức:
\(A=\left[\frac{1}{x^2+2xy+y^2}-\frac{1}{x^2-y^2}\right]:\frac{4xy}{y^2-x^2}\)
Giúp nha m.n! thanks!!!
Ta có: \(A=\left(\frac{1}{x^2+2xy+y^2}-\frac{1}{x^2-y^2}\right):\frac{4xy}{y^2-x^2}\)
\(=\left[\frac{1}{\left(x+y\right)^2}-\frac{1}{\left(x+y\right)\left(x-y\right)}\right].\frac{\left(y+x\right)\left(y-x\right)}{4xy}\)
\(=\frac{1}{x+y}\left(\frac{1}{x+y}-\frac{1}{x-y}\right).\frac{\left(x+y\right)\left(y-x\right)}{4xy}\)
\(=\frac{-2y}{\left(x+y\right)\left(x-y\right)}.\frac{x-y}{-4xy}\)
\(=\frac{1}{\left(x+y\right).2x}\)
Kb với mình nha mn!
Đúng 0
Bình luận (0)
BÀI 1: pttnt
a) x^3y-2x^y+xy b) x^2-9-4xy+y^2
bài 2 cho biểu thức 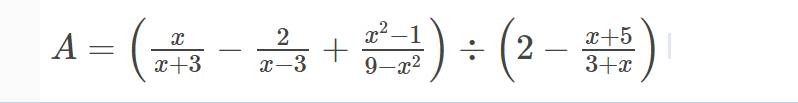
a) Tìm đk xác định của bt A
b) rút gọn bt A
c) tính giá trị của biểu thức A biết x^2-x-2=0
BÀI 1: pttnt
a) x^3y-2x^y+xy b) x^2-9-4xy+y^2
bài 2 cho biểu thức 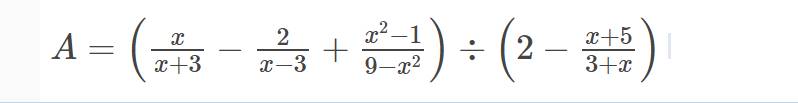
a) Tìm đk xác định của bt A
b) rút gọn bt A
c) tính giá trị của biểu thức A biết x^2-x-2=0
Bài 1:
a: Sửa đề \(x^3y-2x^2y+xy\)
\(=y\left(x^3-2x^2+x\right)\)
\(=x\cdot y\cdot\left(x^2-2x+1\right)\)
\(=xy\left(x-1\right)^2\)
b: Sửa đề: \(x^2-9-2xy+y^2\)
\(=\left(x^2-2xy+y^2\right)-9\)
\(=\left(x-y\right)^2-9\)
\(=\left(x-y-3\right)\left(x-y+3\right)\)
Bài 2:
a: ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)
b: \(A=\left(\dfrac{x}{x+3}-\dfrac{2}{x-3}+\dfrac{x^2-1}{9-x^2}\right):\left(2-\dfrac{x+5}{x+3}\right)\)
\(=\left(\dfrac{x}{x+3}-\dfrac{2}{x-3}-\dfrac{x^2-1}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{2x+6-x-5}{x+3}\)
\(=\dfrac{x\left(x-3\right)-2\left(x+3\right)-x^2+1}{\left(x+3\right)\left(x-3\right)}\cdot\dfrac{x+3}{x+1}\)
\(=\dfrac{x^2-3x-2x-6-x^2+1}{x-3}\cdot\dfrac{1}{x+1}\)
\(=\dfrac{-5x-5}{\left(x-3\right)\left(x+1\right)}=-\dfrac{5\left(x+1\right)}{\left(x-3\right)\left(x+1\right)}=-\dfrac{5}{x-3}\)
c: \(x^2-x-2=0\)
=>\(\left(x-2\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Thay x=2 vào A, ta được:
\(A=\dfrac{-5}{2-3}=\dfrac{-5}{-1}=5\)
Đúng 3
Bình luận (1)
cho công thức
A=(8x^3-y^3)(4x^2-y^2)/(4x^2+2xy)(4x^2-4xy-y^2)
a,Rút gọn biểu thức A
b,Tìm giá trị của A với x=2;y=1/2
a: \(A=\dfrac{\left(2x-y\right)^2\cdot\left(2x+y\right)\left(4x^2+2xy+y^2\right)}{2x\left(2x+y\right)\left(2x-y\right)^2}=\dfrac{4x^2+2xy+y^2}{2x}\)
Đúng 0
Bình luận (1)
Cho biểu thức:Cleft(x-dfrac{4xy}{x+y}+yright):left(dfrac{x}{x+y}+dfrac{y}{y-x}+dfrac{2xy}{x^2-y^2}right)left(xnepm yright)1. Rút gọn biểu thức C ;2. Khi cho left(x^2-y^2right)cdot C-8, hãy tính giá trị của biểu thức:Mx^2left(x+1right)-y^2left(y-1right)-3xyleft(x-y+1right)+xy.
Đọc tiếp
Cho biểu thức:
\(C=\left(x-\dfrac{4xy}{x+y}+y\right):\left(\dfrac{x}{x+y}+\dfrac{y}{y-x}+\dfrac{2xy}{x^2-y^2}\right)\left(x\ne\pm y\right)\)
1. Rút gọn biểu thức \(C\) ;
2. Khi cho \(\left(x^2-y^2\right)\cdot C=-8\), hãy tính giá trị của biểu thức:
\(M=x^2\left(x+1\right)-y^2\left(y-1\right)-3xy\left(x-y+1\right)+xy\).
1: \(C=\left(x-\dfrac{4xy}{x+y}+y\right):\left(\dfrac{x}{x+y}+\dfrac{y}{y-x}+\dfrac{2xy}{x^2-y^2}\right)\)
\(=\dfrac{\left(x+y\right)^2-4xy}{x+y}:\left(\dfrac{x}{x+y}-\dfrac{y}{x-y}+\dfrac{2xy}{\left(x-y\right)\left(x+y\right)}\right)\)
\(=\dfrac{x^2+2xy+y^2-4xy}{x+y}:\dfrac{x\left(x-y\right)-y\left(x+y\right)+2xy}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2-2xy+y^2}{x+y}:\dfrac{x^2-xy-xy-y^2+2xy}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{\left(x-y\right)^2}{x+y}\cdot\dfrac{x^2-y^2}{x^2-y^2}=\dfrac{\left(x-y\right)^2}{x+y}\)
2: \(\left(x^2-y^2\right)\cdot C=-8\)
=>\(\left(x-y\right)\left(x+y\right)\cdot\dfrac{\left(x-y\right)^2}{x+y}=-8\)
=>\(\left(x-y\right)^3=-8\)
=>x-y=-2
=>x=y-2
\(M=x^2\left(x+1\right)-y^2\left(y-1\right)-3xy\left(x-y+1\right)+xy\)
\(=\left(y-2\right)^2\left(y-2+1\right)-y^2\left(y-1\right)-3xy\left(-2+1\right)+xy\)
\(=\left(y-1\right)\left[\left(y-2\right)^2-y^2\right]+3xy+xy\)
\(=\left(y-1\right)\left(-4y+4\right)+4xy\)
\(=-4\left(y-1\right)^2+4y\left(y-2\right)\)
\(=-4y^2+8y-4+4y^2-8y\)
=-4
Đúng 4
Bình luận (1)
Bài 2 Rút gọn
A=(\(x-\frac{4xy}{x+y}+y\)):(\(\frac{x}{x+y}-\frac{y}{x-y}-\frac{2xy}{x^2-y^2}\))
B=(\(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\)):\(\frac{x^2+4x^2y^2+y^4-4}{x^2+y+xy+x}\):\(\frac{1}{2x^2+y+2}\)
Cho biểu thức A=\(\frac{4xy}{y^2-x^2}:\left(\frac{1}{X^2+2xy+y^2}-\frac{x^2-y^2}{x^4-y^4}\right)\)với x khác +-y và y khác 0
1, Rút gọn A và tìm giá trị của x;y để A=0
2,Tìm giá trị của x;y nguyên để A=\(x^2+xy+x+y+1\)