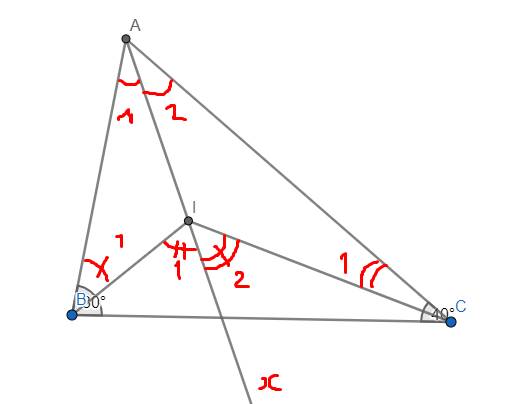
Ta có \(\widehat{I_1}=\widehat{A_1}+\widehat{B_1}\) và \(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\)

\(\Rightarrow\widehat{BIC}=\widehat{I_1}+\widehat{I_2}\)

\(=\left(\widehat{A_1}+\widehat{A_2}\right)+\left(\widehat{B_1}+\widehat{C_1}\right)\)

\(=\widehat{BAC}+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)

\(=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)

\(=180^o-\left(80^o+40^o\right)+\dfrac{80^o+40^o}{2}\)

\(=120^o\)

Vậy \(\widehat{BIC}=120^o\)

B1: Cho tam giác ABC có B=80, C=40 độ. Tia phân giác của góc B cắt AC tại D. Tính ADB.

B2:  Cho ta giác ABC có B-C=20 độ. Đường phân giác AD của góc A cắt BC tại D. Tính ADB  và  ADC.

B3: Cho hình vẽ tính ACB

Bạn nguyen hai anh 

Tham khảo tại đây nhé :

https://olm.vn/hoi-dap/detail/92950113524.html

Hình tự vẽ

Vì tam giác ABC cân tại A => góc B = góc C 

=> \(\widehat{B}=\widehat{C}=\left(180^{\text{o}}-2.70^{\text{o}}\right):2=20^{\text{o}}\)

=> \(\widehat{CBI}=\widehat{BCI}\) = 20 : 2 = 10^o

=> Xét tam giác BIC có : \(\widehat{BIC}=\)180^o - 10^o - 10^o = 160^o

Hình tự vẽ nhé !

Vì tam giác ABC cân tại A \(\Rightarrow\widehat{B}=\widehat{C}\left(1\right)\)

Xét tam giác ABC có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(2\right)\) ( tính chất tổng 3 góc 1 tam giác )

Từ \(\left(1\right)\left(2\right)\Rightarrow\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}=\frac{180^0-70^0}{2}=55^0\)

Vì tia phân giác góc B và C cắt nhau tại I \(\Rightarrow\widehat{BCI}=\widehat{CBI}=55^0\div2=27,5^0\) 

Xét tam giác BIC có \(\widehat{BCI}+\widehat{BIC}+\widehat{CBI}=180^0\) ( t/c tổng 3 góc 1 tam giác )

\(\Rightarrow\widehat{BIC}=180^0-\left(\widehat{BCI}+\widehat{CBI}\right)=180^0-\left(27,5^0+27,5^0\right)=125^0\)

Cậu tự vẽ hình !

Theo tổng ba goác trong một tam giác , ta có :

\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)

\(70^0+\widehat{ABC}+\widehat{ACB}=180^0\)

\(\widehat{ABC}+\widehat{ACB}=110^0\)

Vì I là là giao điểm ba đường phân giác nên 

BI là phân giác của góc ABC

\(\Rightarrow\widehat{ABI}=\widehat{IBC}=\frac{\widehat{ABC}}{2}\)

CI là phân giác của góc ACB

\(\Rightarrow\widehat{ACI}=\widehat{ICB}=\frac{\widehat{ACB}}{2}\)

Ta có :

\(\widehat{IBC}+\widehat{ICB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{100^0}{2}=50^0\)

Và áp dụng tổng 3 góc trong tam giác lên tam giác BIC thì 

=> Góc BIC = 180⁰ - 50⁰ = 130⁰

hỏi gì chạy ra mà hỏi cô 

tttttttt

ta có tam giác abc cân tại a có số đo là 100 độ

=> B =C = (180-100)/2 = 40 độ 

vì hai đường phân giác  của hai góc B và C trong tam giác abc cắt nhau tại i

=> CBI= BCI= 40/2 = 20 độ

vì tổng số đo các góc trong tam giác = 180 độ 

=> BIC = 180 - CBI-BIC= 180 -(20+20) = 140 (độ)