
Những câu hỏi liên quan
-cho 4 gương G1,G2,G3,G4,quay mặt sáng vào nhau thành 4 mặt bên của hình hộp chữ nhật.chính giữa gương G1 có một lỗ nhỏ A.
a)vẽ đường đi của một tia sáng trên mặt phẳng giấy vẽ .đi vào p/x lần lượt lên gương G2,G3,G4 rồi ra ngoài bằng lỗ A
b)tính đường đi của tia sáng trong TH trên .quãng đường đi có phụ thuộc vào vị trí lỗ A hay k?
))) giúp e với. .e đang cần gấp ạ
Đọc tiếp
-cho 4 gương G1,G2,G3,G4,quay mặt sáng vào nhau thành 4 mặt bên của hình hộp chữ nhật.chính giữa gương G1 có một lỗ nhỏ A.
a)vẽ đường đi của một tia sáng trên mặt phẳng giấy vẽ .đi vào p/x lần lượt lên gương G2,G3,G4 rồi ra ngoài bằng lỗ A
b)tính đường đi của tia sáng trong TH trên .quãng đường đi có phụ thuộc vào vị trí lỗ A hay k?
=))) giúp e với. ![]() .e đang cần gấp ạ
.e đang cần gấp ạ
Câu 2: (2 điểm) Hai gương phẳng G1, G2 có mặt phản xạ quay vào nhau và hợp với nhau một góc nhọn a như hình 1.
Chiếu tới gương G1 một tia sáng SI hợp với mặt gương G1 một góc b.
a) Vẽ tất cả các tia sáng phản xạ lần lượt trên hai gương trong trường hợp a450, b300 .
b) Tìm điều kiện để SI sau khi phản xạ hai lần trên G1 lại quay về theo đường cũ.
Đọc tiếp
Câu 2: (2 điểm) Hai gương phẳng G1, G2 có mặt phản xạ quay vào nhau và hợp với nhau một góc nhọn a như hình 1.
Chiếu tới gương G1 một tia sáng SI hợp với mặt gương G1 một góc b.
a) Vẽ tất cả các tia sáng phản xạ lần lượt trên hai gương trong trường hợp a=450, b=300 .
b) Tìm điều kiện để SI sau khi phản xạ hai lần trên G1 lại quay về theo đường cũ.
Cho ba gương phẳng G1; G2 và G3 được ghép thành tam giác cân như hình vẽ. Trên gương G1 có một lỗ nhỏ S người ta chiếu một chùm tia sáng hẹp qua lỗ S vào bên trong theo phương vuông góc với G1. Tia sáng sau khi phản xạ lần lượt trên các gương lại đi ra ngoài theo lỗ S và không bị lệch so với tia chiếu vào.Hãy xác định góc hợp bởi giữa các cặp gương với nhau
Đọc tiếp
Cho ba gương phẳng G1; G2 và G3 được ghép thành tam giác cân như hình vẽ. Trên gương G1 có một lỗ nhỏ S người ta chiếu một chùm tia sáng hẹp qua lỗ S vào bên trong theo phương vuông góc với G1. Tia sáng sau khi phản xạ lần lượt trên các gương lại đi ra ngoài theo lỗ S và không bị lệch so với tia chiếu vào.
Hãy xác định góc hợp bởi giữa các cặp gương với nhau

chúc bạn học tốt1
Ba gương phẳng (G1), (G21), (G3) được lắp thành một lăng trụ đáy tam giác cân như hình vẽTrên gương (G1) có một lỗ nhỏ S. Người ta chiếu một chùm tia sáng hẹp qua lỗ S vào bên trong theo phương vuông góc với (G1). Tia sáng sau khi phản xạ lần lượt trên các gương lại đi ra ngoài qua lỗ S và không bị lệch so với phương của tia chiếu đi vào. Hãy xác định góc hợp bởi giữa các cặp gương với nhau.
Đọc tiếp
Ba gương phẳng (G1), (G21), (G3) được lắp thành một lăng trụ đáy tam giác cân như hình vẽ
Trên gương (G1) có một lỗ nhỏ S. Người ta chiếu một chùm tia sáng hẹp qua lỗ S vào bên trong theo phương vuông góc với (G1). Tia sáng sau khi phản xạ lần lượt trên các gương lại đi ra ngoài qua lỗ S và không bị lệch so với phương của tia chiếu đi vào. Hãy xác định góc hợp bởi giữa các cặp gương với nhau.
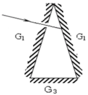
Vì sau khi phản xạ lần lượt trên các gương, tia phản xạ ló ra ngoài lỗ S trùng đúng với tia chiếu vào. Điều đó cho thấy trên từng mặt phản xạ có sự trùng nhau của tia tới và tia ló. Điều này chỉ xảy ra khi tia KR tới gương G3 theo hướng vuông góc với mặt gương. Trên hình vẽ ta thấy
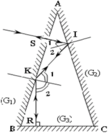
Tại I : I ^ 1 = I ^ 2 = A ^
Tại K: K ^ 1 = K ^ 2
Mặt khác K ^ 1 = I ^ 1 + I ^ 2 = 2 A ^
Do KR^BC ⇒ K ^ 2 = B ^ = C ^
Þ B ^ = C ^ = 2 A ^
Trong DABC có A ^ + B ^ + C ^ = 180 0
A ^ + 2 A ^ + 2 A ^ = 5 A ^ = 180 0 ⇒ A ^ = 180 0 5 = 36 0 ⇒ B ^ = C ^ = 2 A ^ = 72 0
Đúng 0
Bình luận (0)
Hai gương phẳng G1, G2 có mặt phản xạ quay vào nhau và hợp với nhau một góc nhọn a như hình 1. Chiếu tới gương G1 một tia sáng SI hợp với mặt gương G1 một góc b. a) Vẽ tất cả các tia sáng phản xạ lần lượt trên hai gương trong trường hợp a=450, b=300 . b) Tìm điều kiện để SI sau khi phản xạ hai lần trên G1 lại quay về theo đường cũ.
hai gương phẳng G1 và G2 có mặt phản xạ quay vào nhau , hợp với nhau 1 góc ampha . Tia sáng SI đến gương G1 , hợp với mặt phản xạ của gương G1 một góc 30 độ ( hình vẽ ) . Cho tia phản xạ IJ đến gương G2 . Tia sáng này phản xạ trên gương G2 . Cho tia JR , người ta thấy JR // SI . Tìm ampha
hai gương phẳng G1 và G2 có mặt phản xạ quay vào nhau hợp với nhau một góc 120 độ Chiếu một tia sáng tới gương sao cho tia sáng này có thể lần lượt phản xạ trên cả hai gương G1 và G2 vẽ tiếp đường truyền của tia sáng xác định độ lớn của góc hợp bởi tia tới gương G1 và tia phản xạ trên gương g2 và thình bày cách vẽ đường đi của tia sáng tới 2 gương
Hai gương phẳng G1, G2 quay mặt phản xạ vào nhau và tạo với nhau một góc 60 0 600 . Một điểm sáng S nằm trong khoảng 2 gương. a) Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S phản xạ lần lượt qua hai gương G1, G2 rồi quay trở lại S b) Tính góc hợp bởi tia tới xuất phát từ S và tia phản xạ đi qua S Mọi người giúp mình với nha, làm ơn đó . Thanks mọi người nhìu nhìu nè!
Ba gương phẳng quay mặt phản xạ vào nhau tạo với nhau một lăng trụ đáy là tam giác cân ABC. Trên gương G1 có một lỗ thủng, cho tia sáng chiếu vào vuông góc với G1 như hình vẽ. Biết rằng tia sáng này phản xạ lần lượt trên mỗi gương một lần rồi quay trở về đường cũ. Tính các góc tạo bởi các mặt gương. A S I B C G1 giúp mình với mình cần gấp
Đọc tiếp
Ba gương phẳng quay mặt phản xạ vào nhau tạo với nhau một lăng trụ đáy là tam giác cân ABC. Trên gương G1 có một lỗ thủng, cho tia sáng chiếu vào vuông góc với G1 như hình vẽ. Biết rằng tia sáng này phản xạ lần lượt trên mỗi gương một lần rồi quay trở về đường cũ. Tính các góc tạo bởi các mặt gương.
giúp mình với mình cần gấp ![]()
Vì sau khi phản xạ lần lượt trên các gương, tia phản xạ ló ra ngoài lỗ S trùng đúng với tia chiếu vào. Điều đó cho thấy trên từng mặt phản xạ có sự trùng nhau của tia tới và tia ló. Điều này chỉ xảy ra khi tia KR tới gương G3 theo hướng vuông góc với mặt gương. Trên hình vẽ ta thấy
Tại I : ˆI1=ˆI2=ˆAI^1=I^2=A^
Tại K: ˆK1=ˆK2K^1=K^2
Mặt khác ˆK1=ˆI1+ˆI2=2ˆAK^1=I^1+I^2=2A^
Do KR^BC ⇒ˆK2=ˆB=ˆC⇒K^2=B^=C^
Þ ˆB=ˆC=2ˆAB^=C^=2A^
Trong DABC có ˆA+ˆB+ˆC=1800A^+B^+C^=1800
ˆA+2ˆA+2ˆA=5ˆA=1800⇒ˆA=18005=360ˆ⇒B=ˆC=2ˆA=720A^+2A^+2A^=5A^=1800⇒A^=18005=360⇒B^=C^=2A^=720
Đúng 1
Bình luận (2)
Tại I : ˆI1=ˆI2=ˆAI^1=I^2=A^
Tại K: ˆK1=ˆK2K^1=K^2
Mặt khác ˆK1=ˆI1+ˆI2=2ˆAK^1=I^1+I^2=2A^
Do KR^BC ⇒ˆK2=ˆB=ˆC⇒K^2=B^=C^
Þ ˆB=ˆC=2ˆAB^=C^=2A^
Trong DABC có ˆA+ˆB+ˆC=1800A^+B^+C^=1800
ˆA+2ˆA+2ˆA=5ˆA=1800⇒ˆA=18005=360ˆ⇒B=ˆC=2ˆA=720A^+2A^+2A^=5A^=1800⇒A^=18005=360⇒B^=C^=2A^=720
Đúng 0
Bình luận (0)















