cho tam giác ABC cân tại A. Lấy điểm D thuộc AB, E thuộc AC sao cho AD=AE. Chứng minh rằng: DC=BE

Những câu hỏi liên quan
Cho tam giác ABC vuông cân tại A. Lấy E thuộc cạnh AC. Trên tia đối tia AB lấy điểm D sao cho AD = AE. Chứng minh: a) DE vuông góc với BC. b) BE vuông góc DC.
Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC b) BE vuông góc với DC
Tham khảo:
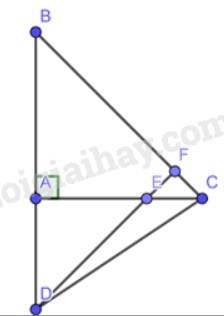
a) Vì tam giác ABC vuông cân tại A
\( \Rightarrow \) \(\widehat B = \widehat C = {45^o}\)(2 góc ở đáy bằng nhau)
Xét tam giác AED có :
AE = AD
AC vuông góc với AB
\( \Rightarrow \) Tam giác AED vuông cân tại A
\( \Rightarrow \widehat {ADE} = \widehat {AED} = {45^o}\)
Mà \(\widehat {AED};\widehat {CEF}\)là 2 góc đối đỉnh \( \Rightarrow \widehat {AED} = \widehat {CEF} = {45^o}\)
Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :
\( \Rightarrow \widehat F + \widehat C + \widehat E = {180^o}\)
\( \Rightarrow \widehat F = {180^o} - {45^o} - {45^o} = {90^o} \Rightarrow EF \bot BC \Rightarrow DE \bot BC\)
b) Vì DE vuông góc với BC \( \Rightarrow \) DE là đường cao của tam giác BCD
Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)
\( \Rightarrow \)BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)
\( \Rightarrow \)BE vuông góc với DC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB < AC. Lấy E thuộc AC sao cho AE=AB. Trên tia đối của tia BA lấy điểm D sao cho BD=EC.
a) Chứng minh rằng tam giác ADC cân tại A.
b) Kẻ AH vuông góc với BE tại H, AH cắt DC tại K. Chứng minh AK là đường trung trực của DC.
Cho tam giác ABC cân tại A. Lấy điểm E thuộc cạnh AB , lấy điểm D thuộc tia đối của tia CA sao cho: AE + AD = AB + AC. Kẻ đường thẳng qua C và song song với DE cắt đường thẳng qua E và song song với DC tại F. Chứng minh rằng: a)C/m tam giác EFC = tam giác CDE . b) C/m tam giác FEB cân
Cho tam giác ABC vuông tại A có AB = AC . Lấy điểm D thuộc cạnh AB , điểm E thuộc cạnh AC sao cho AD = AE . Đường thẳng đi qua D và vuông góc với BE cắt CA tại K. Chứng minh tam giác KDC là tam giác cân.
Cho tam giác ABC có AB < AC. Lấy E thuộc AC sao cho AE=AB. Trên tia đối của tia BA lấy điểm D sao cho BD=EC.
a) Chứng minh rằng tam giác ADC cân tại A.
b) Kẻ AH vuông góc với BE tại H, AH cắt DC tại K. Chứng minh AK là đường trung trực của DC.
Cho tam giác ABC (AB=AC). Lấy điểm D thuộc AB ; E thuộc AC sao cho AD=AE. Chứng minh rằng:
a. BE=CD
b. BE cắt CD tại I. Chứng minh: tam giác AID = tam giác CLE.
c. Tam giác BIC cân; tam giác DIE cân.
d. DE song song BC
Mn giúp e vs.cảm ơn mn nhiều ạ
Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AB, E thuộc cạnh AC sao cho AD = AE.
a) Chứng minh BE = CD.
b) Gọi K là giao điểm của BE và CD. Chứng minh tam giác KBC cân.
c) Chứng minh AK là tia phân giác góc A.
d) Kéo dài AK cắt BC tại H. Cho AB =5 cm, BC = 6 cm. Tính độ dài AH.
Cho tam giác giác ABC vuông tại A có AB = AC. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng đi qua D và vuông góc với BE cắt đường thẳng CA tại K. Chứng minh rằng AK = AC.
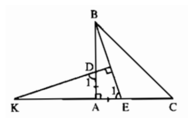

Từ (1) và (2) suy ra AK = AC (điều phải chứng minh ).
Đúng 1
Bình luận (0)

















