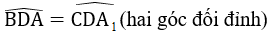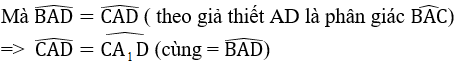Những câu hỏi liên quan
Câu 13: ( Mức 3: 1đ) Một hình tam giác có diện tích 48 cm2, độ dài đáy 12 cm thì chiều cao của tam giác là
A. 2 cm B. 4 cm C. 6 cm D. 8 cm
Xem thêm câu trả lời
Cho tam giác ABC, vuông ở A. Có chu vi là 24cm.Có cạnh AB=2/5 AC;BC=10cm.Tính diện tích hình tam giác ABC
Câu hỏi tương tự Đọc thêm Báo cá
Phần tự luận
Nội dung câu hỏi 1:
Cho tam giác ABC có AB = 6cm; AC = 8 cm; BC = 10 cm
a) Chứng minh tam giác ABC vuông
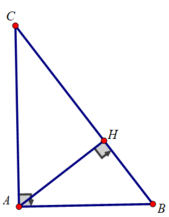
a) Xét tam giác ABC có:
A B 2 + A C 2 = 6 2 + 8 2 = 100 = B C 2
Tam giác ABC vuông tại A.
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (AB≠AC) và O là giao điểm các đường trung trực của tam giác. Vẽ ra phía ngoài của tam giác hai hình vuông ABDE và ACGH. Gọi M, N lần lượt là trung điểm của EH và BC. a) Chứng minh AM vuông góc với BC. b) Trường hợp OH = OE: . Tứ giác AMON là hình gì ? Vì sao ? . Tính góc BAC. Câu hỏi tương tự Đọc thêm Báo cáo Toán lớp 8
Cho tam giác ABC, điểm I nằm trong tam giác. Các tia AI, BI, CI cắt các cạnh đối diện theo thứ tự ở D, E, F. Đường thẳng đi qua I và song song với BC cắt DE, DF theo thứ tự ở N, M. Chứng minh IN = IM
Đúng 0
Bình luận (0)
Câu 1 cho tam giác abc biết a=6, b=4, c=8 độ dài đường cao từ đỉnh A là 3? Diện tích tam giác là?
Câu 2 cho tam giác biết a=4, b=5, góc C= 60. Diện tích tam giác là ?
Câu 3 cho tam giác abc có a2+b2-c2 >0. Khi đó góc C là ?
E mong các ac giúp e bài toán trên nha. E cảm ơn rất nhiều ^^
Câu 1: Diện tích tam giác là: \(\frac{h_A.a}{2}=\frac{3.6}{2}=9\)(đvdt)
Câu 2: Diện tích tam giác là: \(\frac{1}{2}ab.\sin C=\frac{1}{2}.4.5.\sin60^o=5\sqrt{3}\)(đvdt)
Câu 2: Ta có: \(\hept{\begin{cases}c^2=a^2+b^2-2ab.\cos C\\a^2+b^2>c^2\end{cases}\Rightarrow c^2>c^2-2ab.\cos C\Leftrightarrow2ab.\cos C>0}\)
\(\Rightarrow\cos C>0\Rightarrow C< 90^o\)
Vậy C là góc nhọn
Đúng 0
Bình luận (0)
Nhân ngày 8/3, em sẽ lm j trong ngày này.
CÔ EM CHO CÂU HỎI NÀY ĐỪNG BÁO CÁO Ạ, ĐỂ TRÁNH BỊ BÁO CÁO EM CÓ CÂU HỎI 4/12 + 5/3
Chúc mẹ của mình luôn mạnh khỏe, v.v
Đúng 1
Bình luận (0)
- Nhân ngày 8/3, em sẽ phụ giúp mẹ làm những việc nhà mình có thể làm được như rửa bát, quét nhà, giặt quần áo,... Nếu có thời gian, em sẽ làm thiệp tặng mẹ. Mua hoa hồng tặng mẹ để bày tỏ tầm lòng, chúc mẹ những lời chúc tốt đẹp nhất.
- 4/12 + 5/3 = 72/36
Đúng 1
Bình luận (0)
Con thật may mắn, hạnh phúc được là con của mẹ. Con cầu mong mẹ luôn mạnh khỏe, mãi ở bên chúng con. Chúc mừng mẹ ngày 8/3!
 Hơi xấu
Hơi xấu
Đúng 2
Bình luận (5)
Xem thêm câu trả lời
Câu 1 : Cho tam giác ABC có a=3, b=4, c=7 . Tính R
Câu 2 : Cho tam giác ABC có AB=4, BC=6, CA=9 . Tính ma + hb
Câu 1:
Chú ý độ dài 3 cạnh của tam giác là sai thì \(a+b=7=c\)
Nếu là cạnh của tam giác thì: \(\left\{{}\begin{matrix}a+b>c\\a+c>b\\c+b>a\end{matrix}\right.\)
Câu 2: Ta có:
\(m_a=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{AC^2+AB^2}{2}-\dfrac{BC^2}{4}}\)
\(\Rightarrow m_a=\sqrt{\dfrac{9^2+4^2}{2}-\dfrac{6^2}{4}}\)
\(\Rightarrow m_a\approx6,3\)
Ta có: \(p=\dfrac{AB+AC+BC}{2}=\dfrac{4+6+9}{2}=\dfrac{19}{2}\)
\(\Rightarrow S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{\dfrac{19}{2}\cdot\left(\dfrac{19}{2}-6\right)\cdot\left(\dfrac{19}{2}-9\right)\cdot\left(\dfrac{19}{2}-4\right)}\approx9,5\)
\(\Rightarrow h_b=2\cdot\dfrac{S_{ABC}}{b}\Rightarrow h_b=2\cdot\dfrac{9,5}{9}\approx2,1\)
Đúng 1
Bình luận (1)
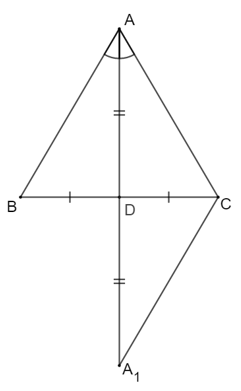
Câu 5: (1đ) CMR nếu tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác
đó là một tam giác cân.
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 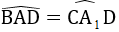
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
HOK T ~
Xét tam giác ABH và tam giác ACH có
\(\hept{\begin{cases}\widehat{AHB}=\widehat{AHC}\left(=90^{\text{o}}\right)\\BH=CH\\AH\text{ chung }\end{cases}\Rightarrow\Delta ABH=\Delta ACH\left(c-g-c\right)}\)
=> AB = AC (cạnh tương ứng)
=> Tam giác ABC cân tại A
Cho tam giác đều ABC như hình 01. Em hãy trả lời các câu hỏi sau:
a) Liệt kê các đỉnh, các cạnh của tam giác ABC.
b) Em có nhận xét gì về độ dài 3 cạnh của tam giác ABC.
A B C Hình 01
Đọc tiếp
Cho tam giác đều ABC như hình 01. Em hãy trả lời các câu hỏi sau:
a) Liệt kê các đỉnh, các cạnh của tam giác ABC.
b) Em có nhận xét gì về độ dài 3 cạnh của tam giác ABC.