1, Do hàm số trên cắt trục hoành tại điểm có hoành độ bằng 3 hay hàm số trên đi qua A(3;0) 

<=> \(0=6+b\Leftrightarrow b=-6\)

2, Hoành độ giao điểm (P) ; (d) tm pt 

\(x^2-\left(m-1\right)x-m+4=0\)

Để (P) cắt (d) tại 2 điểm pb nằm về 2 phía trục tung khi pt có 2 nghiệm trái dấu hay 

\(x_1x_2=-m+4< 0\Leftrightarrow-m< -4\Leftrightarrow m>4\)

a: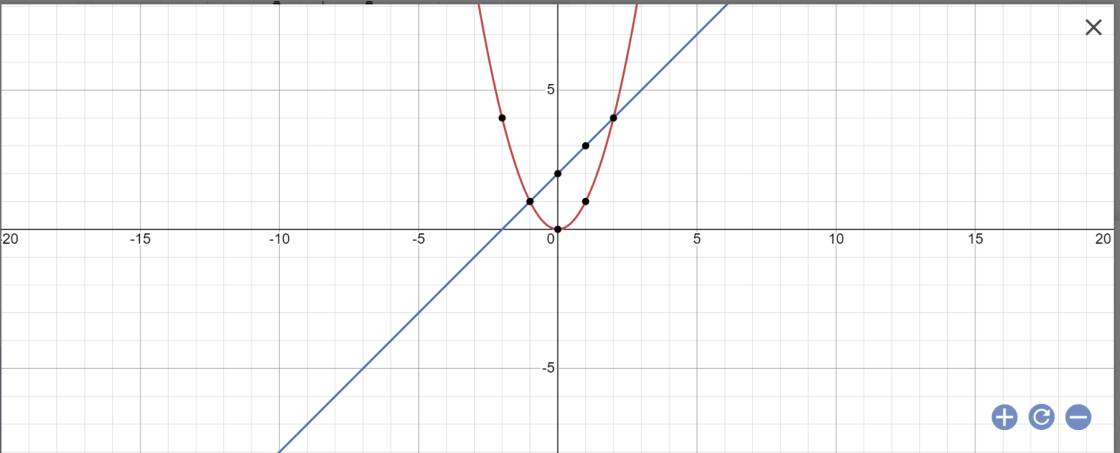 

b: PTHĐGĐ là:

x^2-x-2=0

=>(x-2)(x+1)=0

=>x=2 hoặc x=-1

=>y=4 hoặc y=1

c: PTHĐGĐ là:

x^2-2x+m=0

Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0

2 điểm nằm về 2 phía của trục tung --> 2 no trái dấu

hoành độ giao điểm la no của pt:x^2=4x-m^2+16

                                              <=>x^2-4x+m^2-16=0

Pt có 2 no trái dấu <=> x1.x2<0

                            <=> m^2-16<0 ( ht Vi-et)

                             <=>m^2<16

                              <=>-4<m<4

đã cm đc nó có 2 nghiệm đâu mà dùng Vi-et bạn ơi 

PTHĐGĐ là:

x^2-2x+m-3=0

Để (P) cắt (d) hai điểm phân biệt nằm về hai phía của trục tung thì m-3<0

=>m<3

Lời giải:
a. $(d)$ cắt trục tung tại điểm có tung độ $3$, tức là cắt trục tung tại điểm $(0;3)$

$(0;3)\in (d)$

$\Leftrightarrow 3=(m+2).0+2m^2+1$

$\Leftrightarrow 2m^2=2$
$\Leftrightarrow m^2=1$

$\Leftrightarrow m=\pm 1$

Khi $m=1$ thì ta có hàm số $y=3x+3$

Khi $m=-1$ thì ta có hàm số $y=x+3$ 

Bạn có thể tự vẽ 2 đths này.

b.

Để $(d)$ cắt $(d')$ thì: $m+2\neq 2m+2$

$\Leftrightarrow m\neq 0$

\(a,\Leftrightarrow y=0;x=2\Leftrightarrow2m-2+m-2=0\Leftrightarrow m=\dfrac{4}{3}\)

\(b,\) PT giao Ox: \(\Leftrightarrow\left(m-1\right)x=2-m\Leftrightarrow x=\dfrac{2-m}{m-1}\Leftrightarrow A\left(\dfrac{2-m}{m-1};0\right)\Leftrightarrow OA=\left|\dfrac{2-m}{m-1}\right|\)

PT giao Oy: \(y=m-2\Leftrightarrow B\left(0;m-2\right)\Leftrightarrow OB=\left|m-2\right|\)

\(S_{OAB}=\dfrac{2}{3}\Leftrightarrow\dfrac{1}{2}OA\cdot OB=\dfrac{2}{3}\Leftrightarrow\left|\dfrac{2-m}{m-1}\cdot\left(m-2\right)\right|=\dfrac{4}{3}\\ \Leftrightarrow\left|\dfrac{-\left(m-2\right)^2}{m-1}\right|=\dfrac{4}{3}\Leftrightarrow\left[{}\begin{matrix}\dfrac{-\left(m-2\right)^2}{m-1}=\dfrac{4}{3}\left(1\right)\\\dfrac{-\left(m-2\right)^2}{1-m}=\dfrac{4}{3}\left(2\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow-3m^2+12m-12=4m-4\\ \Leftrightarrow3m^2-9m+9=0\\ \Leftrightarrow m\in\varnothing\\ \left(2\right)\Leftrightarrow-3m^2+12m-12=4-4m\\ \Leftrightarrow3m^2-16m+16=0\\ \Leftrightarrow\left[{}\begin{matrix}m=4\\m=\dfrac{4}{3}\end{matrix}\right.\)

Vậy \(\left[{}\begin{matrix}m=4\\m=\dfrac{4}{3}\end{matrix}\right.\) thỏa đề

\(c,\) Gọi \(E\left(x_0;y_0\right)\) là điểm cần tìm

\(\Leftrightarrow\left(m-1\right)x_0+m-2=y_0\\ \Leftrightarrow mx_0+m-x_0-y_0-2=0\\ \Leftrightarrow m\left(x_o+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-2-x_0=-1\end{matrix}\right.\Leftrightarrow E\left(-1;-1\right)\)