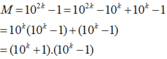Đáp án cần chọn là: D

Ta có:

Vậy M ⋮ 19

10^k - 1 chia hết cho 19 nên 10^k = 19m + 1

k cho mik nha Hiền xinh đẹp ^_<

a﴿ 10^ k ‐ 1 chia hết cho 19 => 10 k ‐ 1 = 19n ﴾n là số tự nhiên﴿

=> 10^ k = 19n + 1 => 10^ 2k = ﴾10^ k ﴿2 = ﴾19n +1﴿2 = ﴾19n +1﴿﴾19n+1﴿ = 361n 2 + 38n + 1

=> 10 2k ‐ 1 = 361n 2 + 38n + 1 ‐ 1 = 361n 2 + 38n chia hết cho 19 => 10 2k ‐ 1 chia hết cho 19

tk nha bạn

thank you bạn

(^_^)

Câu 1: 

Số tổ nhiều nhất có thể chia là UCLN(24;20)

hay số tổ nhiều nhất có thể chia là 4 tổ

Câu 2: 

\(10^{2k}-1=\left(10^k-1\right)\left(10^k+1\right)⋮19\)

a/  10 ^2k - 1 = 10 ^ 2k - 10 ^k + 10 ^ k -1 = 10 ^k(10 ^ k - 1 ) + ( 10 ^ k - 1 ) chia hết cho 19. Bạn hay xem lại các tính chất

b/ 10^3k -1  = 10 ^ 3k - 10 ^k + 10^ k - 1 = 10 ^ k ( 10^2k - 1 ) + ( 10 ^k - 1) chia hết cho 19. xem lại bài a nha. h

nhớ tick nha

(10^k-1)*(10^k+1) cái đó mình ko hiểu lắm

Chọn dãy

1; 11; 111; ... ;111...1 (số cuối có 20 c/s 1)

Chắc chắn trong dãy có 2 số có cùng số dư khi chia cho 19

2 số đó là

111..1(a c/s 1); 11..1(b c/s 1)                   [1< a < b < 20]

=>111..1 - 11..1 chia hết cho 19                                         [b c/s 1 - a c/s 1]

=>111...100...0 chia hết cho 19                                          [b - a c/s 1 ; a c/s 0]

=>11..1 x 10^a chia hết cho 19                                             [b-a c/s 1]

Mà (19;10)=1 =>(19;10^a)=1

=> 111..1 chia hết cho 19 với b-a c/s 1

Câu 3

Giả Sử: k = 4n

=>19⁴ⁿ - 1 = (...1) - 1 = (...0) chia hết cho 10

Vậy có thể tìm đc 1 STN k chia hết cho 10

xét dãy : 19¹,19²,...,19¹¹

các số tự nhiên khi chia cho 10 có 10 ước là: 0,1,2,..,9

Mà dãy số trên có 11 số nên tồn tại ít nhất 2 số tn có cùng số dư khi chia cho 10

gọi 2 số đó là:  19^m và 19ⁿ

(11>m>n>1 m,n=1)

19^m-19ⁿ chia hết cho 10

19ⁿ.(19^m-n -1) chia hết cho 10

mà (10,19)=1 (19ⁿ,10)=1

19^m-n-1 chia hết cho 10

19^k-1 chia hết cho 10 (k=m-n)

19^k-1 chia hết cho 10q

vậy tồn tại 1 số tn k sao cho 19^k-1 chia hết cho 10