gợi ý nè:

thử cộng chúng lại xem

\(\dfrac{x}{y+z+1}\) = \(\dfrac{y}{x+z+2}\) = \(\dfrac{z}{x+y-3}\) = \(x+y+z\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{y+z+1}\)=\(\dfrac{y}{x+z+2}\)=\(\dfrac{z}{x+y-3}\)=\(\dfrac{x+y+z}{y+z+1+x+z+2+x+y-3}\)

\(x+y+z\) = \(\dfrac{x+y+z}{2.\left(x+y+z\right)}\) = \(\dfrac{1}{2}\) (1)

\(\dfrac{x}{y+z+1}\) = \(\dfrac{1}{2}\) ⇒ 2\(x\) = y+z+1 

⇒ 2\(x\) + \(x\) = \(x+y+z+1\) (2)

 Thay (1) vào (2) ta có: 2\(x\) + \(x\) = \(\dfrac{1}{2}\) + 1

                                      3\(x\)      = \(\dfrac{3}{2}\) ⇒ \(x=\dfrac{1}{2}\)

\(\dfrac{y}{x+z+2}\) = \(\dfrac{1}{2}\) ⇒ 2y = \(x+z+2\) ⇒ 2y+y = \(x+y+z+2\) (3)

Thay (1) vào (3) ta có: 2y + y = \(\dfrac{1}{2}\) + 2 

                                   3y = \(\dfrac{5}{2}\) ⇒ y = \(\dfrac{5}{6}\)

Thay \(x=\dfrac{1}{2};y=\dfrac{5}{6}\) vào (1) ta có: \(\dfrac{1}{2}+\dfrac{5}{6}+z\) = \(\dfrac{1}{2}\)

                                                              \(\dfrac{5}{6}\) + z = 0 ⇒ z = - \(\dfrac{5}{6}\)

Kết luận: (\(x;y;z\)) = (\(\dfrac{1}{2}\); \(\dfrac{5}{6}\); - \(\dfrac{5}{6}\))

TH1: x + y + z $\ne$ 0

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{y+z+1}$ = $\frac{y}{x+z+2}$ = $\frac{z}{x+y-3}$ = $\frac{x+y+z}{y+z+1+x+z+2+x+y-3}$ 

              = $\frac{x+y+z}{x+y+z+x+y+z}$ = $\frac{x+y+z}{2(x+y+z)}$ = $\frac{1}{2}$ 

⇒ x + y + z = $\frac{1}{2}$

⇒ x + y       = $\frac{1}{2}$ - z

    x + z        = $\frac{1}{2}$ - y

    y + z        = $\frac{1}{2}$ - x

Thay y + z + 1 = $\frac{1}{2}$ - x + 1

⇒ $\frac{x}{\frac{1}{2}-x+1}$ = $\frac{1}{2}$

⇒ 2x = $\frac{1}{2}$ - x + 1

⇒ 2x + x = $\frac{1}{2}$ + 1

⇒  3x   =  $\frac{3}{2}$

⇒   x    = $\frac{1}{2}$

Thay x + z + 2 = $\frac{1}{2}$ - y + 2

⇒ $\frac{y}{\frac{1}{2}-y+2}$ = $\frac{1}{2}$

⇒ 2y = $\frac{1}{2}$ - y + 2

⇒ 2y + y = $\frac{1}{2}$ + 2

⇒   3y  = $\frac{5}{2}$

⇒     y   = $\frac{5}{6}$

Thay x + y - 3 = $\frac{1}{2}$ - z - 3

⇒ $\frac{z}{\frac{1}{2}-z-3}=$\frac{1}{2}$

⇒ 2z = $\frac{1}{2}$ - z - 3

⇒ 2z + z = $\frac{1}{2}$ - 3

⇒  3z  = $\frac{-5}{2}$

⇒   z   = $\frac{-5}{6}$

TH2: x + y + z = 0

⇒ $\frac{x}{y+z+1}$ = $\frac{y}{x+z+2}$ = $\frac{z}{x+y-3}$ = 0

⇒ x = y = z = 0

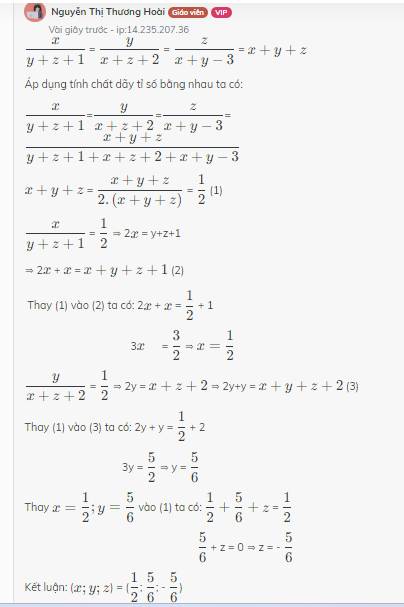
https://olm.vn/cau-hoi/tim-tat-ca-cac-so-xyz-biet-dfracxyz1dfracyxz2dfraczxy-3xyz-giair-chi-tiet-ho-e-vs-a.8297156371934

tổng các số x, y, z là:

2+3+( -5 )=0

số x là:0-3=-3

số y là:0-(-5)=5

số z là:0-2=-2

Ta có (x+y)+(y+z)+(z+x)=2+3+(-5)

         (x+y)+(y+z)+(z+x)=0

         2x+2y+2z=0

         2(x+y+z)=0

         =>x+y+z=0

    Mà x+y=2 => z=0-2=-2

    Mà y+z=3 => y=3-(-2)=5

    Mà z+x=-5 => x= (-5)-(-2)=-3

    Vậy x= -3; y=5; z= -2

Thanks

Bài 1

a) (x + 3)(x + 2) = 0

x + 3 = 0 hoặc x + 2 = 0

*) x + 3 = 0

x = 0 - 3

x = -3 (nhận)

*) x + 2 = 0

x = 0 - 2

x = -2 (nhận)

Vậy x = -3; x = -2

b) (7 - x)³ = -8

(7 - x)³ = (-2)³

7 - x = -2

x = 7 + 2

x = 9 (nhận)

Vậy x = 9

Bài 3

20a + 10b = 2010

10b = 2010 - 20a

b = (2010 - 20a) : 10

*) a = 0

b = (2010 - 20.0) : 10 = 201

*) a = 1

b = (2010 - 10.1) : 10 = 200

*) a = 2

b = (2010 - 10.2) : 10 = 199

Vậy ta có ba cặp số nguyên (a; b) thỏa mãn:

(0; 201); (1; 200); (2; 199)

Ta có: 

\(\hept{\begin{cases}x+y+z=3\\\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{3}\\x^2+y^2+z^2=17\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+y+z=3\\2\left(xy+yz+zx\right)=\frac{2xyz}{3}\\x^2+y^2+z^2=17\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+y+z=3\\2\left(xy+yz+zx\right)=\frac{2xyz}{3}\\\left(x+y+z\right)^2=17+\frac{2xyz}{3}\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+y+z=3\\xy+yz+zx=-4\\xyz=-12\end{cases}}\)

Từ đây ta có x, y, z sẽ là 3 nghiệm của phương trình

\(X^3-3X^2-4X+12=0\) 

\(\Leftrightarrow\left(X-3\right)\left(X-2\right)\left(X+2\right)=0\)

\(\Leftrightarrow\hept{\begin{cases}X=3\\X=2\\X=-2\end{cases}}\)

Vậy các bộ x, y, z thỏa đề bài là: \(\left(x,y,z\right)=\left(-2,2,3;-2,3,2;2,-2,3;2,3,-2;3,2,-2;3,-2,2\right)\)

?????????????????????????

đánh sai đề rồi bạn êi, phải là \(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}=3\Leftrightarrow2x\sqrt{1-y^2}\) \(+2y\sqrt{2-z^2}+2z\sqrt{3-x^2}=6\)

<=> \(\left(x-\sqrt{1-y^2}\right)^2+\left(y-\sqrt{2-z^2}\right)^2+\left(z-\sqrt{3-x^2}\right)^2=0\)

<=> ..bla bla tự làm nhá !

Thanks bạn nhiều nhiều lắm nha

Sử dụng Bất đẳng thức Bunyakovsky cho 2 bộ 3 số \(\left(\sqrt{1-y^2};\sqrt{2-z^2};\sqrt{3-x^2}\right)\) và \(\left(x,y,z\right)\) ta có

\(\left(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}\right)^2\le\left(x^2+y^2+z^2\right)\cdot\left[6-\left(x^2+y^2+z^2\right)\right]\left(1\right)\)

Đặt \(x^2+y^2+z^2=a\) ta có Bất đẳng thức (1) tương đương

\(9=\left(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}\right)^2\le\left(a\right)\cdot\left(6-a\right)\)

\(=-a^2+6a-9+9=-\left(a-3\right)^2+9\le9\)

Dấu "=" xảy ra khi   Giải hệ phương trình trên ta được 

Dấu "=" xảy ra khi \(\hept{\begin{cases}a=x^2+y^2+z^2=3\\\frac{x^2}{1-y^2}=\frac{y^2}{2-z^2}=\frac{z^2}{3-x^2}=1\end{cases}}\)   giải hệ pt ta có \(\hept{\begin{cases}x=1\\y=0\\z=\sqrt{2}\end{cases}}\)

Thế nào nó bị lỗi nên không hiển thị

\(z=\sqrt{2}\)nữa olm bị sao mà lỗi suất vậy

Lời giải:
Áp dụng BĐT Bunhiacopxky:

$\text{VT}(1^2+1^2+1^2)\geq (1+\frac{x}{y+z}+1+\frac{y}{x+z}+1+\frac{z}{x+y})^2$

$\Leftrightarrow 3\text{VT}\geq (3+\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y})^2$

$ = \left[3+\frac{x^2}{xy+xz}+\frac{y^2}{yz+yx}+\frac{z^2}{zy+zx}\right]^2$

$\geq \left[3+\frac{(x+y+z)^2}{2(xy+yz+xz)}\right]^2$

$\geq \left[3+\frac{3(xy+yz+xz)}{2(xy+yz+xz)}\right]^2=\frac{81}{4}$

$\Rightarrow \text{VT}\geq \frac{27}{4}$

Dấu "=" xảy ra khi $x=y=z>0$

Áp dụng BĐT Bunhiacopxky:

VT(12+12+12)≥(1+��+�+1+��+�+1+��+�)2VT(12+12+12)≥(1+y+zx​+1+x+zy​+1+x+yz​)2

⇔3VT≥(3+��+�+��+�+��+�)2⇔3VT≥(3+y+zx​+x+zy​+x+yz​)2

=[3+�2��+��+�2��+��+�2��+��]2=[3+xy+xzx2​+yz+yxy2​+zy+zxz2​]2

≥[3+(�+�+�)22(��+��+��)]2≥[3+2(xy+yz+xz)(x+y+z)2​]2

≥[3+3(��+��+��)2(��+��+��)]2=814≥[3+2(xy+yz+xz)3(xy+yz+xz)​]2=481​

⇒VT≥274⇒VT≥427​

Dấu "=" xảy ra khi $x=y=z>0$