cho tam giác abc vuông tại c có ab = 5cm, oc=3cm, dụng đường tròn (o;oc). qua điểm c kẻ đường thẳng vuông góc với ao tại h và cắt đường tròn tâm o tại b. tính ac, ch, CM AB là tiếp tuyến của(O:OC).

Những câu hỏi liên quan
1. Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình quạt tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^o\)
2. Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm nội tiếp đường tròn (O). Tính diện tích hình tròn (O)
2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB 4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D
Cho tam giác ABC vuông tại A có AB4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D.
a) Tính độ dài đoạn thẳng AH
b) Chứng minh BD là tiếp tuyến của đường tròn (C)
c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua...
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D Cho tam giác ABC vuông tại A có AB=4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D. a) Tính độ dài đoạn thẳng AH b) Chứng minh BD là tiếp tuyến của đường tròn (C) c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB,BD lần lượt tại P,Q. Chứng minh EF bình phương =4PE.QF
a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại C có AB 5cm,ABC 60°, đường cao CK.Vẽ đường tròn tâm O đường kính CK , đường tròn (O ) cắt CB tại P (P khác C) a) Tính độ dài đoạn thẳng BC b) Chứng minh AB là tiếp tuyến của đường tròn (O) c)Tính khoảng cách từ O đến đường thẳng BC d) Từ B vẽ tiếp tuyến thứ hai BH với đường tròn (O) (H là tiếp điểm , H khác K ).Chứng minh tam giác BHP đồng dạng với tam giác BHC.
Đọc tiếp
Cho tam giác ABC vuông tại C có AB =5cm,ABC =60°, đường cao CK.Vẽ đường tròn tâm O đường kính CK , đường tròn (O ) cắt CB tại P (P khác C) a) Tính độ dài đoạn thẳng BC b) Chứng minh AB là tiếp tuyến của đường tròn (O) c)Tính khoảng cách từ O đến đường thẳng BC d) Từ B vẽ tiếp tuyến thứ hai BH với đường tròn (O) (H là tiếp điểm , H khác K ).Chứng minh tam giác BHP đồng dạng với tam giác BHC.
a: Xét ΔABC vuông tại C có
\(BC=AB\cdot\sin30^0=5\cdot\dfrac{1}{2}=2.5\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại C có AB 5cm,ABC 60°, đường cao CK.Vẽ đường tròn tâm O đường kính CK , đường tròn (O ) cắt CB tại P (P khác C)
a) Tính độ dài đoạn thẳng BC
b) Chứng minh AB là tiếp tuyến của đường tròn (O)
c)Tính khoảng cách từ O đến đường thẳng BC
d) Từ B vẽ tiếp tuyến thứ hai BH với đường tròn (O) (H là tiếp điểm , H khác K ).Chứng minh tam giác BHP đồng dạng với tam giác BHC.
Đọc tiếp
Cho tam giác ABC vuông tại C có AB =5cm,ABC =60°, đường cao CK.Vẽ đường tròn tâm O đường kính CK , đường tròn (O ) cắt CB tại P (P khác C)
a) Tính độ dài đoạn thẳng BC
b) Chứng minh AB là tiếp tuyến của đường tròn (O)
c)Tính khoảng cách từ O đến đường thẳng BC
d) Từ B vẽ tiếp tuyến thứ hai BH với đường tròn (O) (H là tiếp điểm , H khác K ).Chứng minh tam giác BHP đồng dạng với tam giác BHC.
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D và E. Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm.
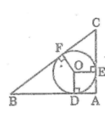
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
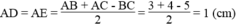
Đúng 0
Bình luận (0)
cho tam giác vuông ABC vuông tại A , ba nử đường tròn có đường kính là AB= 3cm, AC =4cm , BC= 5cm , Tính diện tích phần gạch chéo
giúp mik giải nhé
diện tích hình tròn có đường kính là 5 cm là:5:2*5:2*3,14=19,625(cm2).diện tích hình tam giác là:3*4:2=6(cm2).diện tích hai ửa hình tròn nhỏ là:19,625 - 6=13,625(cm2).diện tích hình tròn lớn là:(3:2*3:2*3,14)+(4:2*4:2*3,14)=19,625(cm2).diện tích phần tô đậm là:19.625 -13,625=6(cm2)
)
Đúng 1
Bình luận (0)
cho tam giác abc có ab=3cm, ac=4cm, bc=5cm. kẻ ah vuông góc với bc( h thuộc bc). a/ tam giác abc là tam giác gì? vì sao. b/ tính ah, góc b và c. c/ vẽ đường tròn( b, bh) và đường tròn ( c, ch). từ điểm a lần lượt vẽ tiếp tuyến am và an của đường tròn( b) và (c). tính góc mhn
a. \(BC^2=AB^2+AC^2\) nên ABC vuông tại A
b. Hệ thức lượng: \(AH=\dfrac{AB\cdot AC}{BC}=2,4\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx37^0\)
Đúng 3
Bình luận (0)
cho tam giác abc vuông tại a có ab=3cm ac=5cm đường phân giác ad . đường vuông góc dc cắt ac ở ea, tam giác abc đồng dạng tam giác becb, tính bc, bd,ad
Xem chi tiết
a:
Sửa đề tam giác DEC
Xet ΔABC vuông tại A và ΔDEC vuông tại D có
góc C chung
=>ΔABC đồng dạng với ΔDEC
b: \(BC=\sqrt{3^2+5^2}=\sqrt{34}\left(cm\right)\)
\(AD=\dfrac{2\cdot3\cdot5}{3+5}\cdot cos45=\dfrac{15\sqrt{2}}{8}\left(cm\right)\)
AD là phân giác
=>BD/AB=CD/AC
=>\(\dfrac{BD}{3}=\dfrac{CD}{5}=\dfrac{\sqrt{34}}{8}\)
=>\(BD=\dfrac{3\sqrt{34}}{8}\left(cm\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH biết BC=10cm, góc C=30 độ
a) Tính AB,AC và AH
b) Vẽ đường tròn tâm O đường kính AB. Chứng minh H thuộc đường tròn O
c) Vẽ AI vuông góc với OC tại I và cắt đường tròn tại D. Chứng minh CD là tiếp tuyến của đừng tròn O

















