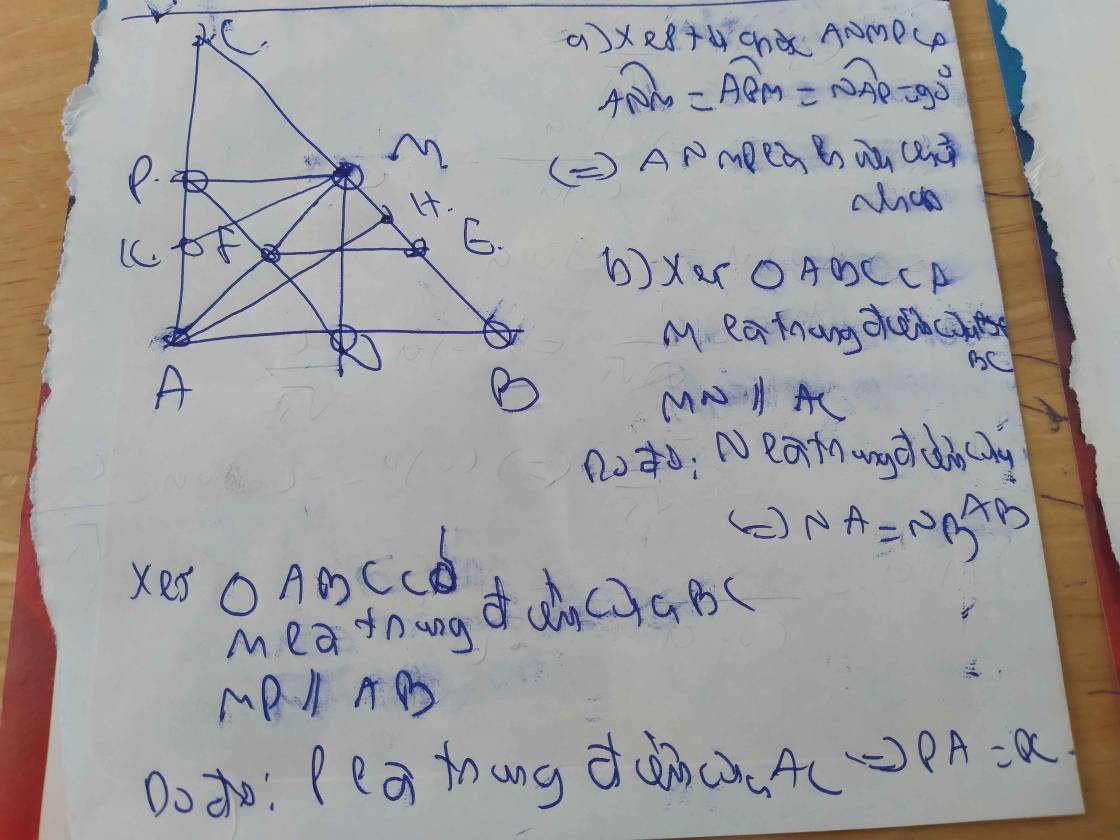
cho tam giác ABC vuông tại A có AN là đường trung tuyến . kẻ MN vuông góc với AB tại MNP vuông góc với AC tại P a) chứng minh tứ giác AMNP là hcn b)tứ giác ANCE là hình gì ?vì sao?c) ME cắt AN tại I , cắt AC tại Q . c/m 3IQ nhỏ hơn NC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, trung tuyến AM. Kẻ MD vuông góc với AB tại D; ME vuông góc với AC tại E.
a) Tứ giác ADME là hình gì? Vì sao?
b) Gọi I là điểm đối xứng với M qua D. Chứng minh tứ giác AMBI là hình thoi.
c) Tìm điều kiện của tam giác ABC để tứ giác AMBI là hình vuông.
d) Vẽ đường cao AH của tam giác ABC, kẻ HP vuông góc với AB tại P, HQ vuông góc với AC tại
Q. Chứng minh PQ vuông góc với AM.
Giúp mình câu d nhé!
Đọc tiếp
Cho tam giác ABC vuông tại A, trung tuyến AM. Kẻ MD vuông góc với AB tại D; ME vuông góc với AC tại E.
a) Tứ giác ADME là hình gì? Vì sao?
b) Gọi I là điểm đối xứng với M qua D. Chứng minh tứ giác AMBI là hình thoi.
c) Tìm điều kiện của tam giác ABC để tứ giác AMBI là hình vuông.
d) Vẽ đường cao AH của tam giác ABC, kẻ HP vuông góc với AB tại P, HQ vuông góc với AC tại
Q. Chứng minh PQ vuông góc với AM.
Giúp mình câu d nhé!
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ ME vuông góc AB tại E, MF vuông góc AC
tại F.
a) Tứ giác AEMF là hình gì? Vì sao?
b) Chứng minh F là trung điểm của AC
c)
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ ME vuông góc AB tại E, MF vuông góc AC tại F.
a) Tứ giác AEMF là hình gì? Vì sao?
b) Chứng minh F là trung điểm của AC
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật
b: ta có: MF\(\perp\)AC
AB\(\perp\)AC
Do đó: MF//AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=8cm, AC=6cm, đường trung tuyến AI.
Kẻ IE vuông góc với AB tại E, IK vuông góc với AC tại K.
a. Tính độ dài AI.
b. Chứng minh tứ giác AEIK là hình chữ nhật.
c. Tứ giác EICK là hình gì? Vì sao?
d. Kẻ AH vuông góc với BC tại H. Gọi O là giao điểm của AI và EK. Chứng
minh tam giác OHE là tam giác cân.
Cho tam giác ABC vuông tại A (AB AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC)a) Tứ giác ANMP là hình gì? vì sao?b) Chứng minh: NANB, PAPC và tứ giác BMPN là hình bình hànhc) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. chứng minh - Tứ giác ABEF là hình thang când) Kẻ AH vuông góc với BC ; MK // AH (K thuộc AC). Chứng minh rằng BK vuông góc với HN.
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC)
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NA=NB, PA=PC và tứ giác BMPN là hình bình hành
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. chứng minh
- Tứ giác ABEF là hình thang cân
d) Kẻ AH vuông góc với BC ; MK // AH (K thuộc AC). Chứng minh rằng BK vuông góc với HN.
Cho tam giác ABC vuông tại A (AB AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC)
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NANB, PAPC và tứ giác BMPN là hình bình hành
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. chứng minh
- Tứ giác ABEF là hình thang cân
- Tứ giác MENF là hình thoi
d) Kẻ AH vuông góc với BC ; MK // AH (K thuộc AC). Chứng minh rằng BK vuông góc với HN.
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC)
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NA=NB, PA=PC và tứ giác BMPN là hình bình hành
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. chứng minh
- Tứ giác ABEF là hình thang cân
- Tứ giác MENF là hình thoi
d) Kẻ AH vuông góc với BC ; MK // AH (K thuộc AC). Chứng minh rằng BK vuông góc với HN.
Cho tam giác ABC vuông tại A (AB AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC)
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NANB, PAPC và tứ giác BMPN là hình bình hành
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. chứng minh
- Tứ giác ABEF là hình thang cân
d) Kẻ AH vuông góc với BC ; MK // AH (K thuộc AC). Chứng minh rằng BK vuông góc với HN.
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC)
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NA=NB, PA=PC và tứ giác BMPN là hình bình hành
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. chứng minh
- Tứ giác ABEF là hình thang cân
d) Kẻ AH vuông góc với BC ; MK // AH (K thuộc AC). Chứng minh rằng BK vuông góc với HN.
a/
\(MP\perp AC;NA\perp AC\) => MP//NA
\(MN\perp AB;PA\perp AB\) => MN//PA
=> ANMP là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có \(\widehat{A}=90^o\)
=> ANMP là hình chữ nhật (hbh có 1 góc vuông là HCN)
b/
MN//PA (cmt) => MN//AC
MB=MC (gt)
=> NA=NB (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
C/m tương tự cũng có PA=PC
Ta có
MP//NA (cmt) => MP//NB
NA=NB; PA=PC => NP là đường trung bình của tg ABC
=> NP//BC => NP//MB
=> BMPN là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
c/
Xét HCN ANMP có
FM=FA (trong HCN 2 đường chéo cắt nhau tại trung điểm mỗi đường)
EM=EB (gt)
=> EF là đường trung bình của tg MAB => EF//AB
=> ABEF là hình thang
Ta có
MB=MC => AM=MB=MC=BC/2 (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Ta có
FM=FA=AM/2
EB=EM=BM/2
=> FA=EB
=> ABEF là hình thang cân
d/
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, trung tuyến AM.
a) Cho AB = 6 cm, AC = 8 cm. Tính độ dài AM.
b) Kẻ MD vuông góc với AB, ME vuông góc với AC. Tứ giác ADME là hình gì? Vì
sao?
c) Tứ giác DECB là hình gì? Vì sao?
d) Gọi H, I lần lượt là trung điểm của BM và CM. Chứng minh rằng: DH = EI.
e) Tam giác ABC cần có thêm điều kiện gì để tứ giác ADME là hình vuông?
Cho tam giác ABC vuông tại A . Đường trung tuyến AN. Điểm M là hình chiếu vuông góc của N trên AB . Vẽ điểm Q đối xứng với điểm N qua AC . Gọi giao điểm của NQ và AC là P.1) Các tứ giác AMNP,ANCQ là hình gì ?Vì sao ?2) AN cắt MP tại điểm E. Chứng minh : ba điểm B,E,Q thẳng hàng.3) Tam giác ABC có thêm điều kiện gì để tứ giác ABCQ là hình thang cân.giúp mik với ạ , mình cảm ơn
Đọc tiếp
Cho tam giác ABC vuông tại A . Đường trung tuyến AN. Điểm M là hình chiếu vuông góc của N trên AB . Vẽ điểm Q đối xứng với điểm N qua AC . Gọi giao điểm của NQ và AC là P.
1) Các tứ giác AMNP,ANCQ là hình gì ?Vì sao ?
2) AN cắt MP tại điểm E. Chứng minh : ba điểm B,E,Q thẳng hàng.
3) Tam giác ABC có thêm điều kiện gì để tứ giác ABCQ là hình thang cân.
giúp mik với ạ , mình cảm ơn
1: Ta có: N và Q đối xứng nhau qua AC
nên AC là đường trung trực của NQ
Suy ra: P là trung điểm của NQ và AC\(\perp\)NQ tại P
Xét tứ giác AMNP có
\(\widehat{PAM}=\widehat{APN}=\widehat{AMN}=90^0\)
Do đó: AMNP là hình chữ nhật
Xét ΔABC có
N là trung điểm của BC
NP//AB
Do đó: P là trung điểm của AC
Xét tứ giác ANCQ có
P là trung điểm của AC
P là trung điểm của NP
Do đó: ANCQ là hình bình hành
mà AC\(\perp\)NQ
nên ANCQ là hình thoi
Đúng 0
Bình luận (0)