giải giùm em gấp câu 2 với ạ em cần rất gấp em cảm ơn ạ

Những câu hỏi liên quan
Giúp em bài 8 vs ạ em đang cần gấp pleaseeeeeeeee
Giải chi tiết ra giùm em ạ em cảm ơn nhìu 
 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Mọi người ơi, giải giúp em bài nào cũng được ạ, em đang cần gấp ạ, em cảm ơn rất nhiều ạ.
8.31:
a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
XétΔBAC có BM/BA=BN/BC
nên MN//AC
=>MN vuông góc BD
=>MN vuông góc MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc NMQ=90 độ
=>MNPQ là hình chữ nhật
=>M,N,P,Q cùng nằm trên 1 đường tròn
Đúng 0
Bình luận (0)
Giúp em với ạ em đang cần gấp ạ.Em cảm ơn rất nhiều ạ
Ai biết giải câu nào thì giải giúp em với ạ em đang cần gấp ý cảm ơn mọi người nhiều ạ


Bài 11:
\(PTHH:2A+Cl_2\rightarrow2ACl\\TheoĐLBTKL:\\ m_A+m_{Cl_2}=m_{ACl}\\ \Leftrightarrow 9,2+m_{Cl_2}=23,4\\ \Rightarrow m_{Cl_2}=23,4-9,2=14,2\left(g\right)\\ n_{Cl_2}=\dfrac{14,2}{71}=0,2\left(mol\right)\\ n_A=2.0,2=0,4\left(mol\right)\\ M_A=\dfrac{9,2}{0,4}=23\left(\dfrac{g}{mol}\right)\\ \Rightarrow A\left(I\right):Natri\left(Na=23\right)\)
Đúng 1
Bình luận (0)
mọi người ai giải hộ em câu này với em đang cần gấp câu này em cảm ơn ạ!

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
3.15:
EF vuông góc MH
NP vuông góc MH
Do đó: EF//NP
3.17:
góc yKH+góc H=180 độ
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ky//Hx
Đúng 0
Bình luận (0)
Mọi người giúp em giải câu 4 với ạ, em cần gấp cảm ơn nhiều.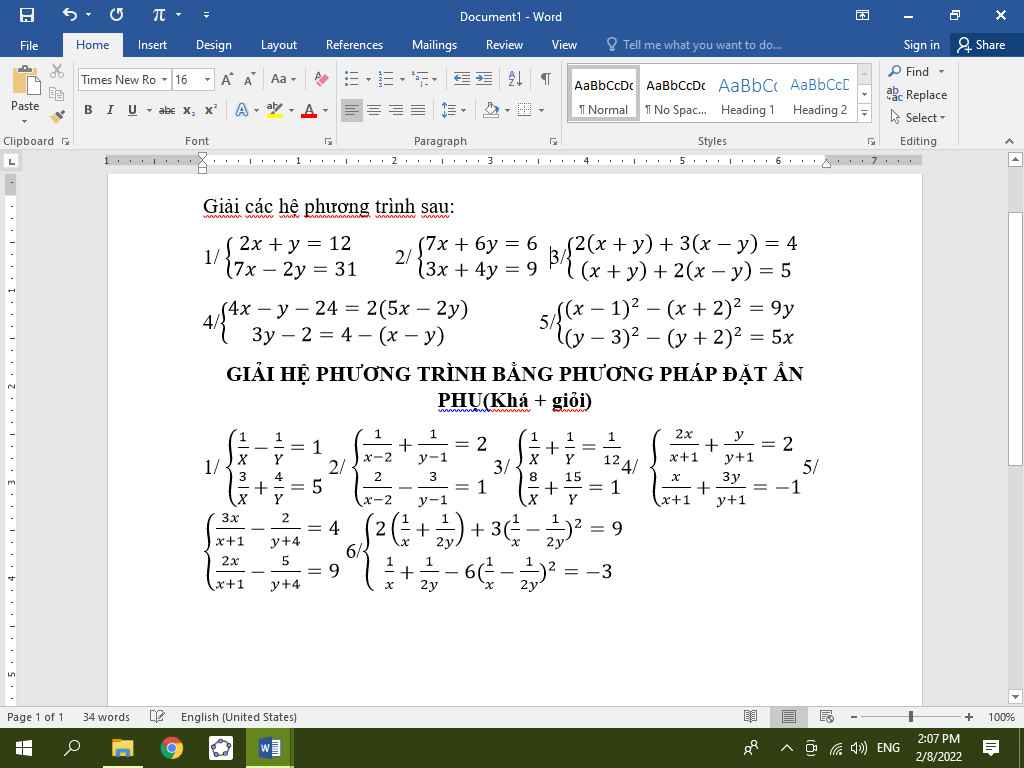

1, \(\left\{{}\begin{matrix}4x+2y=24\\7x-2y=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=55\\y=12-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)
2, thiếu đề
4, \(\left\{{}\begin{matrix}4x-y-24=10x-4y\\3y-2=4-x+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\x+2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\-6x-12y=-36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15y=60\\x=6-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Em cần gấp 2 câu này để mai nộp ạ có ai giải giúp em được không em cảm ơn ạ.














