Tìm tất cả giá trị của tham số m để phương trình |2x-5m| = 2x-3m có nghiệm

Những câu hỏi liên quan
Tìm tất cả giá trị của tham số m để phương trình
4
x
+
2
x
+
4
3
m
(
2
x
+
1
)
có hai nghiệm phân biệt. A.
1
m
≤
log
3
4
B.
1
m
log
3...
Đọc tiếp
Tìm tất cả giá trị của tham số m để phương trình 4 x + 2 x + 4 = 3 m ( 2 x + 1 ) có hai nghiệm phân biệt.
A. 1 < m ≤ log 3 4
B. 1 < m < log 3 4
C. log 3 4 ≤ m < 1
D. log 3 4 < m < 1
tìm tất cả các giá trị của tham số m để phương trình sau √x^2 + 2x +3m = 2x+1 có hai nghiệm phân biệt
\(PT\Leftrightarrow x^2+2x+3x=4x^2+4x+1\\ \Leftrightarrow3x^2+2x+1-3m=0\\ \text{PT có 2 nghiệm pb}\Leftrightarrow\Delta'>0\\ \Leftrightarrow1-3\left(1-3m\right)>0\\ \Leftrightarrow1+9m-1>0\Leftrightarrow m>0\)
Đúng 2
Bình luận (1)
tìm tất cả các giá trị của tham số m để phương trình sau √x^2 + 2x +3m = 2x+1 có hai nghiệm phân biệt
\(PT\Leftrightarrow x^2+2x+3m=4x^2+4x+1\\ \Leftrightarrow3x^2+2x+1-3m=0\)
PT có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'=1-3\left(1-3m\right)>0\)
\(\Leftrightarrow9m-2>0\\ \Leftrightarrow m>\dfrac{2}{9}\)
Vậy PT có 2 nghiệm pb \(\Leftrightarrow m>\dfrac{2}{9}\)
Đúng 0
Bình luận (0)
Tìm tất cả giá trị thực của tham số m để bất phương trình
4
x
-
m
.
2
x
+
1
+
3
-
3
m
≤
0
có nghiệm thực. A.
m
≥
2
B.
m
≤
3
C.
m
≤
5...
Đọc tiếp
Tìm tất cả giá trị thực của tham số m để bất phương trình 4 x - m . 2 x + 1 + 3 - 3 m ≤ 0 có nghiệm thực.
A. m ≥ 2
B. m ≤ 3
C. m ≤ 5
D. m ≥ 1

Vậy để bất phương trình có nghiệm thực thì m ≥ 1
Đúng 0
Bình luận (0)
Cho phương trình
4
x
2
-
2
x
+
1
-
m
.
2
x
2
-
2
x
+
2
+
3
m
-
2
0...
Đọc tiếp
Cho phương trình 4 x 2 - 2 x + 1 - m . 2 x 2 - 2 x + 2 + 3 m - 2 = 0 với m là tham số thực. Tìm tất cả các giá trị của m để phương trình có bốn nghiệm phân biệt.
A. m < 1
B. m < 1; m > 2
C. m ≥ 2
D. m > 2
Tìm tất cả các giá trị của tham số thực m để phương trình
m
2
-
3
m
+
2
x
+
m
-
1
0
có nghiệm thực duy nhất. A.
m
≠
1...
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để phương trình m 2 - 3 m + 2 x + m - 1 = 0 có nghiệm thực duy nhất.
A. m ≠ 1 m ≠ 2
B. m ≠ 1
C. m ≠ 2
D. m ≠ 1 hoặc m ≠ 2
Chọn đáp án A
Phương trình đã cho có nghiệm duy nhất khi và chỉ khi 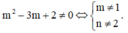
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
3
x
-
2
x
+
1
3
m
-
2
m
+
1
chỉ có 1 nghiệm A. Với mọi m B.
m
≠
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 3 x - 2 x + 1 = 3 m - 2 m + 1 chỉ có 1 nghiệm
A. Với mọi m
B. m ≠ 1
C. m ≠ 1 4
D. Không có giá trị nào của m
Tìm tất cả các giá trị thực của tham số m để phương trình
3
x
-
2
x
+
1
3
m
-
2
m
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 3 x - 2 x + 1 = 3 m - 2 m + 1 chỉ có 1 nghiệm.
A. Với mọi m
B. ![]()
C. ![]()
D. Không có giá trị nào của m.
Đáp án B
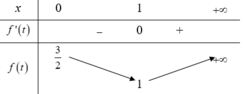
Từ bảng biến thiên của hàm số ![]() ta được kết quả
ta được kết quả 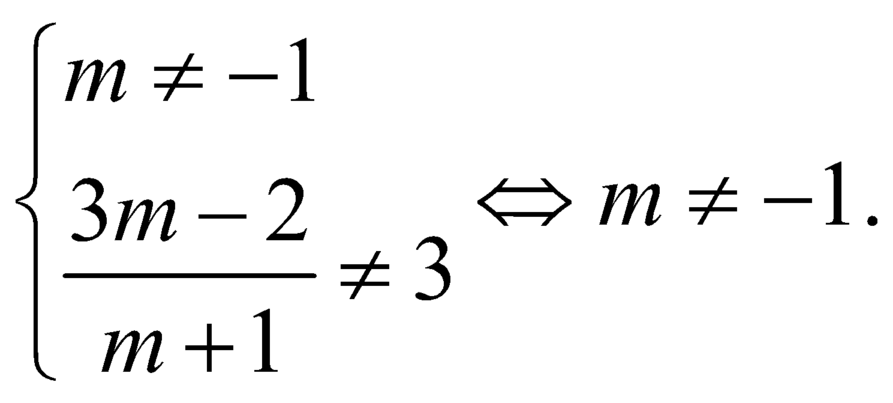
Đúng 0
Bình luận (0)
Cho phương trình
4
x
2
-
2
x
+
1
-
m
.
2
x
2
-
2
x
+
2
+
3
m
-
2
0...
Đọc tiếp
Cho phương trình 4 x 2 - 2 x + 1 - m . 2 x 2 - 2 x + 2 + 3 m - 2 = 0 . Tập tất cả các giá trị của tham số m để phương trình đã cho có nghiệm phân biệt là
A. 2 ; + ∞
B. [ 2 ; + ∞ )
C. 1 ; + ∞
D. - ∞ ; 1 ∪ 2 ; + ∞
![]()
![]()
Xét hàm ![]() trên
trên ![]()

Phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi phương trình (*) có hai nghiệm phân biệt lớn hơn 1 và khác ![]()
Chọn A.
Đúng 0
Bình luận (0)








