
Những câu hỏi liên quan
(2x+3)(x-3)+x(x-2)=3(x-2)(x-2)
hãy giải phương trình trên!!
Ta có : \(\left(2x+3\right)\left(x-3\right)+x\left(x-2\right)=3\left(x-2\right)\left(x-2\right)\)
\(\Leftrightarrow2x^2-3x-9+x^2-2x=3\left(x^2-4x+4\right)\)
\(\Leftrightarrow3x^2-5x-9=3x^2-12x+12\)
\(\Leftrightarrow-5x+12x=12+9\)
\(\Leftrightarrow7x=21\)
\(\Leftrightarrow x=3\)
Vậy \(x=3\)là nghiệm của phương trình .
3.15 giải các phương trình sau :
a) ( x - 6 ) ( 2x - 5 ) ( 3x + 9 ) = 0
b) 2x( x - 3 ) + 5( x - 3 ) = 0
c) ( x^2 - 4 ) - ( x - 2 ) ( 3 - 2x ) =0
3.16 tìm m để phương trình sau có nghiệm :
x=-7 ( 2m - 5 )x - 2m^2 + 8
3.17 giải các phương trình sau :
a) ( 2x - 1 )^2 - ( 2x + 1 ) = 0
\(a,\left(x-6\right)\left(2x-5\right)\left(3x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x-6=0\Leftrightarrow x=6\\2x-5=0\Leftrightarrow x=\dfrac{5}{2}\\3x+9=0\Leftrightarrow x=-3\end{matrix}\right.\)
\(b,2x\left(x-3\right)+5\left(x-3\right)=0\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-3=0\Leftrightarrow x=3\\2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\end{matrix}\right.\)
\(c,x^2-4-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
\(x=-7\left(2m-5\right)x-2m^2+8\Leftrightarrow x+7\left(2m-5\right)=8-2m^2\Leftrightarrow x\left(14m-34\right)=8-2m^2\)
\(ycđb\Leftrightarrow14m-34\ne0\Leftrightarrow m\ne\dfrac{34}{14}\)\(\Rightarrow x=\dfrac{8-2m^2}{14m-34}\)
\(3.17\Leftrightarrow4x^2-4x+1-2x-1=0\Leftrightarrow4x^2-6x=0\Leftrightarrow x\left(4x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
3.15:
a, \(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\2x-5=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\x=\dfrac{5}{2}\\x=-\dfrac{9}{3}=-3\end{matrix}\right.\)
b, \(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
c, \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
3.16
\(\Leftrightarrow\left(2m-5\right).-7-2m^2+8=0\)
\(\Leftrightarrow-14m+35-2m^2+8=0\)
\(\Leftrightarrow-14m-2m^2+43=0\)
\(\Leftrightarrow-2\left(7m+m^2\right)=-43\)
\(\Leftrightarrow m\left(7-m\right)=\dfrac{43}{2}\)
\(\Leftrightarrow\dfrac{m\left(7-m\right)}{1}-\dfrac{43}{2}=0\)
\(\Leftrightarrow\dfrac{14m-2m^2}{2}-\dfrac{43}{2}=0\)
pt vô nghiệm
Đúng 1
Bình luận (0)
giải bất phương trình 2x-3/x-1<1/3
giải bất phương trình 2x-3/x-1 > 1/3
\(\dfrac{2x-3}{x-1}< \dfrac{1}{3}\left(đk:x\ne1\right)\)
\(\Leftrightarrow6x-9< x-1\Leftrightarrow5x< 8\Leftrightarrow x< \dfrac{8}{5}\) và ĐK \(x\ne1\)
\(\dfrac{2x-3}{x-1}>\dfrac{1}{3}\left(đk:x\ne1\right)\)
\(\Leftrightarrow x-1< 6x-9\Leftrightarrow5x>8\Leftrightarrow x>\dfrac{8}{5}\) và ĐK \(x\ne1\)
Đúng 1
Bình luận (0)
Giải phương trình chứa ẩn ở mẫu:a) 4x 2/3x-6-x/2-x=1 3x/2x-4; b) x-3/x 3-x 3/x-3=3/x2-9Các bạn hãy giúp mik với.
Xem chi tiết
Giải phương trình chứa ẩn ở mẫu:a) 4x 2/3x-6-x/2-x=1 3x/2x-4b) x-3/x 3-x 3/x-3=3/x2-9Các bạn hãy giúp mik với:))
Đúng 0
Bình luận (1)
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Đúng 1
Bình luận (0)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
Đúng 1
Bình luận (0)
Giải phương trình ( giải theo trường hợp phương trình chứa biến ở mẫu)
a) 3 phần x-2 = 2x-1 phần x-2 -x
b) x+2 phần x = 2x+3 phần 2x-4
a: \(\Leftrightarrow\dfrac{3}{x-2}=\dfrac{2x-1}{x-2}-\dfrac{x\left(x-2\right)}{x-2}\)
=>3=2x-1-x^2+2x
=>3=-x^2+4x-1
=>x^2-4x+1+3=0
=>x^2-4x+4=0
=>x=2(loại)
b: =>(x+2)(2x-4)=x(2x+3)
=>2x^2-4x+4x-8=2x^2+3x
=>3x=-8
=>x=-8/3(nhận)
Đúng 0
Bình luận (0)
Giải các phương trình sau :
x-2/x+2 + 3/x-2 = x^2-11/x^2-4.
x/2x-6 - x/2x+2 = 2x/(x+1)(x-3).
Xin hãy giúp mình!
\(\frac{x-2}{x+2}+\frac{3}{x-2}=\frac{x^2-11}{x^2-4}\left(x\ne\pm2\right)\)
\(\Leftrightarrow\frac{x-2}{x+2}+\frac{3}{x-2}-\frac{x^2-11}{x^2-4}=0\)
<=> \(\frac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}+\frac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\frac{x^2-11}{\left(x-2\right)\left(x+2\right)}=0\)
<=> \(\frac{x^2-4x+4}{\left(x-2\right)\left(x+2\right)}+\frac{3x+6}{\left(x-2\right)\left(x+2\right)}-\frac{x^2-11}{\left(x-2\right)\left(x+2\right)}=0\)
<=> \(\frac{x^2-4x+4+3x+6-x^2+11}{\left(x-2\right)\left(x+2\right)}=0\)
<=> \(\frac{-x+21}{\left(x-2\right)\left(x+2\right)}=0\)
=> -x+21=0
<=> -x=-21
<=> x=21 (tmđk)
Vậy x=21 là nghiệm của pt
\(\frac{x}{2x-6}-\frac{2}{2x+2}=\frac{2x}{\left(x+1\right)\left(x-3\right)}\left(x\ne-1;x\ne3\right)\)
<=> \(\frac{x}{2x-6}-\frac{2}{2x+2}-\frac{2x}{\left(x+1\right)\left(x-3\right)}=0\)
<=> \(\frac{x}{2\left(x-3\right)}-\frac{2}{2\left(x+1\right)}-\frac{2x}{\left(x+1\right)\left(x-3\right)}=0\)
<=> \(\frac{\left(x+1\right)^2}{2\left(x+1\right)\left(x-3\right)}-\frac{2\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}-\frac{2x\cdot2}{\left(x+1\right)\left(x-3\right)2}=0\)
<=> \(\frac{x^2+2x+1}{2\left(x+1\right)\left(x-3\right)}-\frac{2x-6}{2\left(x+1\right)\left(x-3\right)}-\frac{4x}{2\left(x+1\right)\left(x-3\right)}=0\)
<=> \(\frac{x^2+2x+1-2x-6-4x}{2\left(x+1\right)\left(x-3\right)}=0\)
<=> \(\frac{x^2-4x-5}{2\left(x+1\right)\left(x-3\right)}=0\)
=> x2-4x-5=0
<=> x2-5x+x-5=0
<=> x(x-5)+(x-5)=0
<=> (x-5)(x+1)=0
\(\Leftrightarrow\orbr{\begin{cases}x-5=0\\x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=5\\x=-1\end{cases}}}\)
Đối chiếu điều kiện => x=5
Vậy x=5 là nghiệm của pt
Giải phương trình và bất phương trình sau:
a
)
|
3
x
|
x
+
6
b
)
x
+
2
x
-
2
-
1
x
2
x...
Đọc tiếp
Giải phương trình và bất phương trình sau:
a ) | 3 x | = x + 6 b ) x + 2 x - 2 - 1 x = 2 x x - 2 c ) ( x + 1 ) ( 2 x – 2 ) – 3 > – 5 x – ( 2 x + 1 ) ( 3 – x )
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
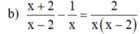
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
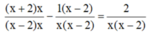
![]()
![]()
![]()
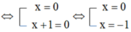
![]()
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
Đúng 0
Bình luận (0)
Khi giải phương trình
2
-
3
x
-
2
x
-
3
3
x
+
2
2
x
+
1
, bạn Hà làm như sau:Theo định nghĩa hai phân thức bằng nhau, ta có:...
Đọc tiếp
Khi giải phương trình 2 - 3 x - 2 x - 3 = 3 x + 2 2 x + 1 , bạn Hà làm như sau:
Theo định nghĩa hai phân thức bằng nhau, ta có:
2 - 3 x - 2 x - 3 = 3 x + 2 2 x + 1
⇔ (2 – 3x)(2x + 1) = (3x + 2)(- 2x – 3)
⇔ -6 x 2 + x + 2 = -6 x 2 – 13x – 6
⇔ 14x = - 8
⇔ x = - 4/7
Vậy phương trình có nghiệm x = - 4/7 .
Em hãy nhận xét về bài làm của bạn Hà.
Đáp số của bài toán đúng nhưng lời giải của bạn Hà chưa đầy đủ.
Lời giải của bạn Hà thiếu bước tìm điều kiện xác định và bước đối chiếu giá trị của x tìm được với điều kiện để kết luận nghiệm.
Trong bài toán trên thì điều kiện xác định của phương trình là:
x ≠ - 3/2 và x ≠ - 1/2
So sánh với điều kiện xác định thì giá trị x = - 4/7 thỏa mãn.
Vậy x = - 4/7 là nghiệm của phương trình.
Đúng 0
Bình luận (0)





















