
Những câu hỏi liên quan
Bài 1: Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA
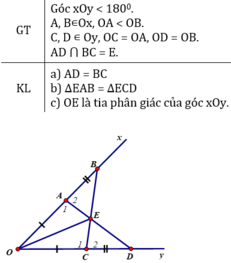
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
OE là tia phân giác của góc xOy
ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒  (hai góc tương ứng)
(hai góc tương ứng)
Vậy OE là tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Cho góc xoy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA< OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC chứng minh rằng. A) AD= BC B) ∆EAB= ∆ECD C)OE là tia phân giác của góc xOy. Giải giúp e câu C với ạ.
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy
Đúng 1
Bình luận (0)
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
a) AD = BC
b) ΔEAB = ΔECD
c) OE là tia phân giác của góc xOy
a)
ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
Đúng 1
Bình luận (0)
c) Ta có:
ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: BOE=DOE
hay OE là tia phân giác của góc xOy
Đúng 1
Bình luận (0)
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
AD = BC
ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
Đúng 1
Bình luận (0)
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
ΔEAB = ΔECD
Do ΔOAD = ΔOCB (chứng minh trên)
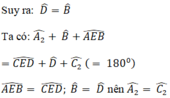
OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
Xét ΔAEB và ΔCED có:
∠B = ∠D
AB = CD
∠A2 = ∠C2
⇒ΔAEB = ΔCED (g.c.g)
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA nhỏ hơn OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB.Hai đường thẳng AD và BC cắt nhau tại I.Chứng minh AC//BD
Xét ΔODB có
\(\dfrac{OA}{OB}=\dfrac{OC}{OD}\)
Do đó: AC//BD
Đúng 0
Bình luận (0)
Bài 1: Cho góc xOy khác góc bẹt lấy các điểm A, B thuộc tia Ox sao cho OA < OB.
Lấy điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB.
Gọi E là giao điểm của AD và BC. Chứng minh:
a) AD = BC b) DEAB = DECD c) OE là phân giác của góc xOy
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt. Lấy điểm A,B thuộc Ox sao cho OA<OB, lấy C,D thuộc Oy sao cho OA=OD, AB=CD
Chứng minh rằng:
a, AD=BC
b, Tam giác EAB= Tam giác ECD
c, OE là tia phân giác của góc xOy

















