cho tam giác abc vuông tại a, m thuộc b. Gọi d và e lần lượt là chân đường vuông góc, kẻ đường vuông góc m từ ab và ac
a/ so sánh am và be
b/ tìm vị trí của điểm m để de có độ dài nhỏ nhất
Những câu hỏi liên quan
cho tam giác abc vuông tại a, m thuộc b. Gọi d và e lần lượt là chân đường vuông góc, kẻ đường vuông góc m từ ab và ac
a/ so sánh am và be
b/ tìm vị trí của điểm m để de có độ dài nhỏ nhât
a: Sửa đề: So sánh AM với DE
Xét tứ giác ADME có \(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
nên ADME là hình chữ nhật
=>DE=AM
b: Kẻ AH là đường cao của ΔABC
Ta có: ΔAHM vuông tại H
=>AH<=AM
mà AM=DE
nên AH<=DE
Dấu '=' xảy ra khi H trùng với M
hay M là chân đường cao kẻ từ A xuống BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC
a) So sánh các độ dài AM, DE
b) Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất
a)Xét tứ giác ADME có góc MDA=90(gt)
góc DAE=90(gt)
góc AEM=90(gt)
=>tứ giác ADME là hình chữ nhật
=>AM=DE
b)Kẻ AH vuông góc với BC
Ta có DE=AM>=AH
Dấu "=" xãy ra khi M trùng H
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường cao kẻ từ A đến BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,M thuộc BC.Gọi D,E lần lượt là chân đường vuông góc kẻ từ M đến AB,ACa,so sánh AM và DEb,tìm vị trí của M trên BC sao cho DE có độ dài nhỏ nhấtc,gọi I là trung điểm của DE,chứng minh khi M chạy trên BC thì I luôn cách BC một khoảng không đổid,khi M trùng HH là chân đường vuông góc kẻ từ A xuống BC,qua A kẻ đường vuông góc với DE cắt BC tại N.chứng minh N là trung điểm của BC e,phát biểu định lý đảo ở câu d và chứng minh
Đọc tiếp
Cho tam giác ABC vuông tại A,M thuộc BC.Gọi D,E lần lượt là chân đường vuông góc kẻ từ M đến AB,AC
a,so sánh AM và DE
b,tìm vị trí của M trên BC sao cho DE có độ dài nhỏ nhất
c,gọi I là trung điểm của DE,chứng minh khi M chạy trên BC thì I luôn cách BC một khoảng không đổi
d,khi M trùng H<H là chân đường vuông góc kẻ từ A xuống BC>,qua A kẻ đường vuông góc với DE cắt BC tại N.chứng minh N là trung điểm của BC
e,phát biểu định lý đảo ở câu d và chứng minh
Em tham khảo bài toán tương tự tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
Chú ý rằng: EF//BC, EF, BC đều cố định nên khoảng cách giữa 2 đường thẳng này là cố định.
Vậy thì I luôn cách BC một khoảng cố định.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có M thuộc cạnh huyền BC. Gọi D và E là chân đường vuông góc. Kẻ từ M đến AB và AC.
Tìm vị trí của M trên bBC để DE có độ dài nhỏ nhất. Tính độ dài nhỏ nhất đó biết AB=15cm, AC=20cm
Cho tam giác ABC vuông ở A, M là một điểm thuộc cạnh huyền BC. Gọi D và E theo thứ tự là chân đường vuông góc kẻ từ M đến AB , AC.
a) So sánh độ dài AM và DE
b) Gọi I là trung điểm của DE. Khi M chuyển động trên BC thì I chuyển động trên đường nào ? Vì sao ?
c) Tìm vị trí của M trên BC để DE nhỏ nhất
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
hihihihihihiihiihiihihiihihihihihihihihihihihihihihiihihiihihihihihihiihihihihihihihihihihihihihihihihhihihihihihihihhiihihihihihiihihiihihihihihihihihihihihihihihihihiihihihihihiihihihihihihihihihiihihihihiihiihihihihiihihihihihiihihihihihiihhiihihihiihihihihihiihihihihhiihhiihiihihihihihihihihihihihiihhiiihhiihhiihihihihihihihiihihih
cho tam giác ABC vuông tại A .M thuộc BC. Gọi D,E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB,AC
a) Tứ giác ADME là hình gì
b) Gọi I là trung điểm của DE. chứng minh rằng ba điểm A,I,M thẳng hàng
c) tìm vị trí của điểm M để DE có độ dài nhỏ nhất
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. GỌi D,E theo thứ tự là chân đường vuông góc kẻ từ M đến AB, AC. Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất
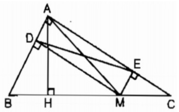
Ta có: AH ⊥ BC nên AM ≥ AH (quan hệ đường vuông góc và đường xiên)
Dấu “=” xảy ra khi M trùng với H
Mà DE = AM ( chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC
a. So sánh độ dài Am, DE
b. Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất.
Làm ơn giúp mình ms mai mình nộp bài rồi ạ =(((
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, điểm M bất kì trên cạnh huyền BC. Gọi D, E lần lượt là hình chiếu của M lên AB, AC
a,CMR tứ giác ADME là HCN
b,Kẻ đường cao AH của tam giác ABC. CMR góc DHE vuông
c,Tìm vị trí điểm M để đoạn thẳng DE có độ dài ngắn nhất
a: Xét tứ giác ADME có
gócADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
b: góc AHM=góc AEM=góc ADM=90 độ
=>A,D,H,M,E cùng thuộc đường tròn đường kính AM
mà ED và AM cùng là đường kính của đường tròn đường kính AM(ED=AM)
nên H nằm trên đường tròn đường kính DE
=>góc DHE=90 độ
c: DE=AM
AM>=AH
=>DE>=AH
Dấu = xảy ra khi M trùng với H
=>M là chân đường cao kẻ từ A xuống BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Điểm M thuộc cạnh huyền BC. Gọi D và E là chân các đường vuông góc kẻ từ M đến AB và AC.
a) Tứ giác ADME là hình gì? Vì sao?
b) Gọi I là trung điểm của DE. Chứng minh 3 điểm A; I; M thẳng hàng
c) Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất? Tính độ dài nhỏ nhất đó nếu AB = 15cm và AC = 20cm
Em tham khảo bài toán tương tự tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)