P ¯ là mệnh đề “15 chia hết cho 3”; P sai,  P ¯ đúng

P ¯ là mệnh đề “15 chia hết cho 3”; P sai,  P ¯ đúng

a) \(\overline{P}\) là mệnh đề " 15 chia hết cho 3"; P sai, \(\overline{P}\) đúng

b) \(\overline{Q}\) là mệnh đề "\(\sqrt{2}\le1\)"; Q đúng, \(\overline{Q}\) sai

Mệnh đề π < 3, 15 đúng vì π = 3,141592654…

Mệnh đề phủ định: "π ≥ 3, 15"

Mệnh đề ‘’|–125| ≤ 0’’ sai vì |–125| = 125 > 0

Mệnh đề phủ định: "|–125| > 0"

Mệnh đề “√2 là số hữu tỉ’’ sai vì √2 là số vô tỉ

Mệnh đề phủ định: "√2 không phải là một số hữu tỉ"

Mệnh đề phủ định của P: P− “ π không là một số hữu tỉ”.

P là mệnh đề sai, P− là mệnh đề đúng.

Mệnh đề phủ định của Q: Q− “Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh thứ ba”.

Q là mệnh đề đúng, Q− là mệnh đề sai.

Mệnh đề sai, vì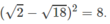 

    Phủ định là 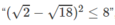 mệnh đề này đúng.

a: Có 1 giá trị x thuộc tập R thỏa mãn x^2=-10

Mệnh đề này sai vì x^2>=0>-10 với mọi x thuộc R

b: Với mọi x thực, x^2+x+12 luôn khác 0

x^2+x+12

=x^2+x+1/4+47/4

=(x+1/2)^2+47/4>=47/4>0 với mọi x

=>Mệnh đề này đúng

c: Với mọi x thuộc R thì x^2 luôn ko lớn hơn 0

Mệnh đề này sai vì ví dụ như x=1 thì 1^2>0 chứ ko bé hơn 0

d: Có một giá trị thực của x thỏa mãn x^2<=0

Mệnh đề này đúng bởi vì có x=0 thỏa mãn x^2<=0

e:

Có một giá trị x thực thỏa mãn x^2+x+5>0

Mệnh đề này đúng vì x^2+x+5=(x+1/2)^2+19/4>0 với mọi x

f: Với mọi giá trị x thực thì x^2+x+5 luôn dương

Mệnh đề này đúng