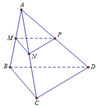
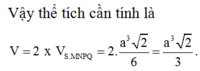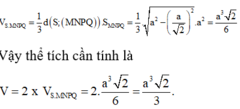Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số : \(\dfrac{V_{\left(H\right)}}{V_{ABCD}}\) ?

Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là \(\dfrac{a}{2}\). Khi đó :
\(V_{ABCD}=a^3\dfrac{\sqrt{2}}{12};V_{\left(H\right)}=\dfrac{1}{3}\left(\dfrac{a}{2}\right)^3\sqrt{2}=a^3\dfrac{\sqrt{2}}{24}\)
Từ đó suy ra :
\(\dfrac{V_{\left(H\right)}}{V_{ }ABCD}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD và ba điểm M, N,P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là: A. Một tam giác B. Một ngũ giác C. Một đoạn thẳng D. Một tứ giác
Đọc tiếp
Cho tứ diện ABCD và ba điểm M, N,P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là:
A. Một tam giác
B. Một ngũ giác
C. Một đoạn thẳng
D. Một tứ giác
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng
M
N
P
là A. Một tam giác B. Một ngũ giá C. Một đoạn thẳng D. Một tứ giác
Đọc tiếp
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng M N P là
A. Một tam giác
B. Một ngũ giá
C. Một đoạn thẳng
D. Một tứ giác
Đáp án A
Hiển nhiên thiết diện của hình tứ diện A B C D khi cắt bởi mặt phẳng M N P là một tam giác
Đúng 0
Bình luận (0)
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là A. Một tam giác B. Một ngũ giá C. Một đoạn thẳng D. Một tứ giác
Đọc tiếp
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là
A. Một tam giác
B. Một ngũ giá
C. Một đoạn thẳng
D. Một tứ giác
Đáp án A
Hiển nhiên thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là một tam giác.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho tứ diện ABCD với A(-1;-2;4), B(-4;-2;0), C(3;-2;1), D(1;1;1). Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D bằng
A. 3
B. 1
C. 2
D. 1 2
Cho tứ diện ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
Đọc tiếp
Cho tứ diện ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
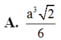
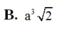
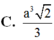

Cho tứ diện ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD. A.
a
3
2
6
B.
a
3
2
C.
a
3
2
3
D.
2...
Đọc tiếp
Cho tứ diện ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
A. a 3 2 6
B. a 3 2
C. a 3 2 3
D. 2 a 3 2 9
Đáp án C

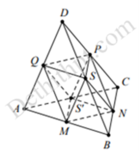
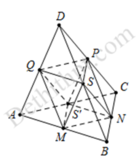
Khối bát diện đều có cạnh là a.
Chia bát diện đều thành hai hình chóp tứ giác đều có tất cả các cạnh bằng a.
Thể tích khối chóp tứ giác đều S.MNPQ là
V S . M N P Q = 1 3 d S ; M N P Q . S M N P Q = 1 3 . a 2 − a 2 2 . a 2 = a 3 2 6
Vậy thể tích cần tính là:
V = 2 x V S . M N P Q = 2. a 3 2 6 = a 3 2 3 .
Đúng 0
Bình luận (0)
Cho tứ diện ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
Đọc tiếp
Cho tứ diện ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
![]()
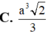
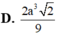
Cho tứ diện đều ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
Đọc tiếp
Cho tứ diện đều ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
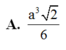
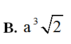
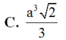
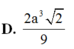
Cho tứ diện đều ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD. A.
a
3
2
6
B.
a
3
2
C.
a
3
2
3
D.
2...
Đọc tiếp
Cho tứ diện đều ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
A. a 3 2 6
B. a 3 2
C. a 3 2 3
D. 2 a 3 2 9
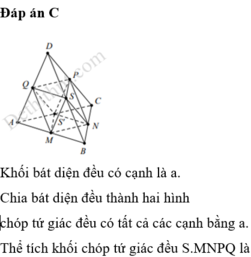
Đáp án C
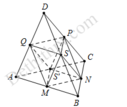
Khối bát diện đều có cạnh là a.
Chia bát diện đều thành hai hình chóp tứ giác đều có tất cả các cạnh bằng a.
Thể tích khối chóp tứ giác đều S.MNPQ là

Đúng 0
Bình luận (0)