Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau: A(2; 3; 4), B(6; 0; 4)

Những câu hỏi liên quan
Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau: A(4; -1; 1), B(2; 1; 0)
Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau :
a) \(A\left(4;-1;1\right);B\left(2;1;0\right)\)
b) \(A\left(2;3;4\right);B\left(6;0;4\right)\)
a) \(\left|\overrightarrow{AB}\right|=3\)
b) \(\left|\overrightarrow{AB}\right|=5\)
Đúng 0
Bình luận (0)
Xác định lực tương tác giữa hai điện tích điểm
q
1
và
q
2
cách nhau một khoảng r trong điện môi
ε
, với các trường hợp sau:a)
q
1
4
.
10
-
8
C
;
q
2
-
8
.
10...
Đọc tiếp
Xác định lực tương tác giữa hai điện tích điểm q 1 và q 2 cách nhau một khoảng r trong điện môi ε , với các trường hợp sau:
a) q 1 = 4 . 10 - 8 C ; q 2 = - 8 . 10 - 8 C ; r = 4cm; ε = 2
b) q 2 = - 0 , 06 μ C ; q 2 = - 0 , 09 μ C ; r = 3cm; ε = 5
a) q 1 = 4 . 10 - 8 C ; q 2 = - 8 . 10 - 8 C ; r = 4cm; ε = 2
Lực tương tác giữa chúng là lực hút và có độ lớn:

b) q 2 = - 0 , 06 μ C ; q 2 = - 0 , 09 μ C ; r = 3cm; ε = 5
Lực tương tác giữa chúng là lực đẩy và có độ lớn:

Đúng 0
Bình luận (0)
Hai điện tích điểm A và B cách nhau 5cm trong chân không có hai điện tích q1 = +16.10-8 C và q2 = - 9.10-8 C. Tính cường độ điện trường tổng hợp và vẽ vectơ cường độ điện trường tại điểm C nằm cách A một khoảng 4cm và cách B một khoảng 3cm.
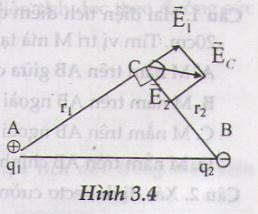
13. Hai điện tích điểm A và B cách nhau 5cm trong chân không có hai điện tích q1 = +16.10-8 C và q2 = - 9.10-8 C. Tính cường độ điện trường tổng hợp và vẽ vectơ cường độ điện trường tại điểm C nằm cách A một khoảng 4cm và cách B một khoảng 3cm.
Hướng dẫn giải.
Đặt AC = r1 và BC = r2 . Gọi −→E1E1→ và −→E2E2→ lần lượt là cường độ điện trường do q1 và q2 gây ra ở C (Hình 3.4).
E1=k.q1εr21E1=k.q1εr12= 9.105 V/m (Hướng theo phương AC).
E1=k.q2εr22E1=k.q2εr22 = 9.105 V/m (Hướng theo phương CB).
Vì tam giác ABC là tam giác vuông nên hai vectơ −→E1E1→ và −→E2E2→ vuông góc với nhau.
Gọi −→ECEC→ là vectơ cường độ điện trường tổng hợp :
−→ECEC→ = −→E1E1→ + −→E2E2→ => EC=√2E1=12,7.105EC=2E1=12,7.105 V/m.
Vectơ −→ECEC→ làm với các phương AC và BC những góc 450 và có chiều như hình vẽ.
Đúng 0
Bình luận (0)
Để đo khoảng cách giữa hai điểm B và C trong đó B không tới được . Người ta xác định các điểm A, D,E như hình vẽ. Sau đó đo được khoảng cách giữa A và C là AC = 9m, Khoảng cách giữa D và C là DC= 6m khoảng cách giữa E và D là DE = 4m Khoảng các giữa hai điểm B và C là bao nhiêu
Chọn từ hoặc cụm từ : (1) trùng nhau; (2) 0; (3) độ dài đoạn thẳng; (4) khoảng cách giữa hai điểm; (5) cách, điền vào chỗ trống thích hợp trong mỗi câu sau đây để diễn đạt đúng về độ dài đoạn thẳng.
a) AB 2 (cm) còn nói là .......A và B bằng 2(cm) hoặc nói là ...............AB bằng 2 (cm) hoặc A...........B một khoảng bằng 2 (cm)
b) Hai điểm A và B trùng nhau còn nói là ......A và B bằng ..........hoặc A...............B một khoảng bằng ......hoặc ...........AB bằng ...........
c) AB 0 còn...
Đọc tiếp
Chọn từ hoặc cụm từ : (1) trùng nhau; (2) 0; (3) độ dài đoạn thẳng; (4) khoảng cách giữa hai điểm; (5) cách, điền vào chỗ trống thích hợp trong mỗi câu sau đây để diễn đạt đúng về độ dài đoạn thẳng.
a) AB = 2 (cm) còn nói là .......A và B bằng 2(cm) hoặc nói là ...............AB bằng 2 (cm) hoặc A...........B một khoảng bằng 2 (cm)
b) Hai điểm A và B trùng nhau còn nói là ......A và B bằng ..........hoặc A...............B một khoảng bằng ......hoặc ...........AB bằng ...........
c) AB = 0 còn nói là ............A và B bằng .........hoặc hai điểm A và B ............hoặc ...........AB bằng ..............hoặc A .............B một khoảng bằng ...........
a) AB = 2 (cm) còn nói là ..(4)..A và B bằng 2(cm) hoặc nói là ..(3)..AB bằng 2 (cm) hoặc A ..(5)..B một khoảng bằng 2 (cm)
b) Hai điểm A và B trùng nhau còn nói là ..(4)..A và B bằng ..(2)..hoặc A ..(5)..B một khoảng bằng ..(2)..hoặc ..(3)..AB bằng ..(2)..
c) AB = 0 còn nói là ..(4)..A và B bằng ..(2)..hoặc hai điểm A và B ..(1)..hoặc ..(3)..AB bằng ..(2)..hoặc A ..(5)..B một khoảng bằng ..(2)..
Đúng 0
Bình luận (0)
cho a, b thuộc Z. Gọi d là khoảng cách giữa hai điểm a và b trên trục số. Hãy so sánh d với b - a trong các trường hợp sau:
a = 12, b = 19 a = -3, b = +11a = -7, b = 6 a = -14, b = -5Ba điểm O, A, B thuộc đường thẳng xy. Tính độ dài đoạn thẳng AB trong 2 trường hợp sau biết OA + OB = a và OA - OB = b, (0<b <a).
TH1: Điểm O nằm giữa 2 điểm A và B.
TH2: Điểm B nằm giữa hai điểm O và A.
TH1 AB = {2;3;4;5;6;....}
TH2 AB = {1;2;3;4;5;....}
Đúng 0
Bình luận (0)
Để đo khoảng cách giữa hai điểm a và b ( không thể đo trực tiếp). Người ta xác định các điểm C, D, E như hình vẽ. sau đó đó được khoảng cách giữa A và C là AC 6m; khoảng cách giữa C và E là EC 2m; khoảng cách giữa E và D là DE 3m. Tính khoảng cách hai điểm A và B. A C E D B
Đọc tiếp
Để đo khoảng cách giữa hai điểm a và b ( không thể đo trực tiếp). Người ta xác định các điểm C, D, E như hình vẽ. sau đó đó được khoảng cách giữa A và C là AC = 6m; khoảng cách giữa C và E là EC = 2m; khoảng cách giữa E và D là DE = 3m. Tính khoảng cách hai điểm A và B.
DE//AB
=>DE/AB=CE/CA
=>3/AB=2/6=1/3
=>AB=9m
Đúng 3
Bình luận (0)

















