
giải chi tiết và giải thích rõ ràng giúm mình ạ, mình phải nộp trước 9h sáng mai ạ
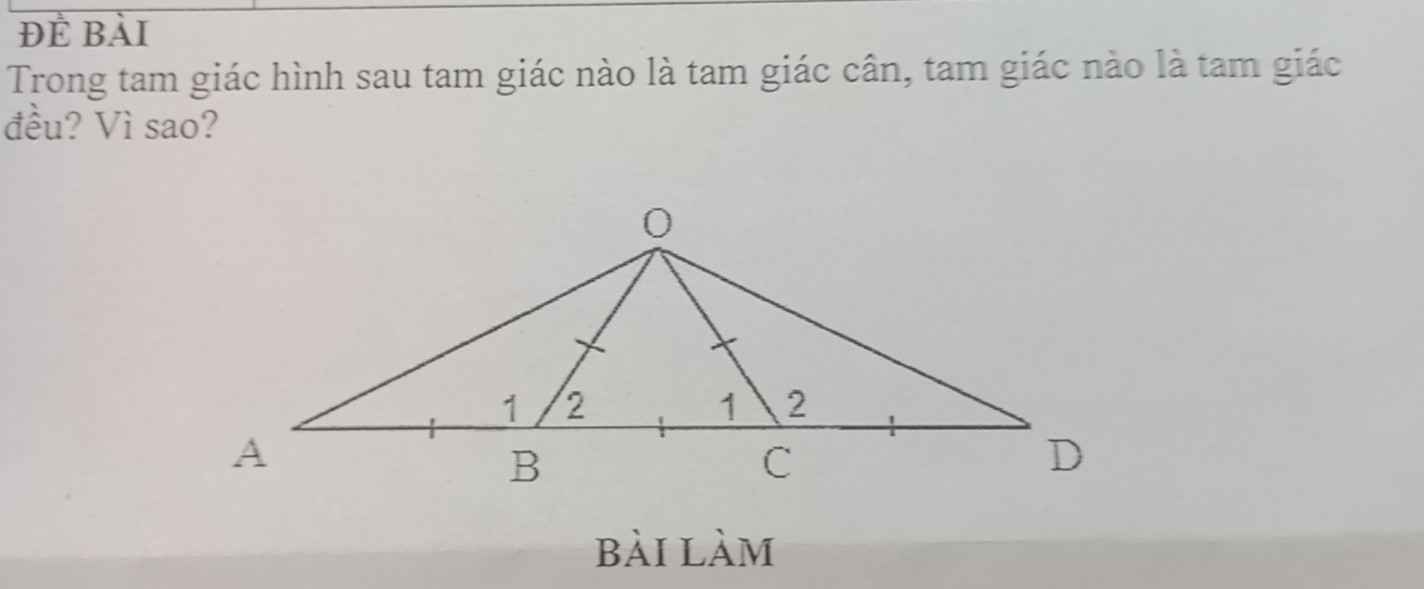
giúp mình chi tiết rõ ràng,giải thích chi tiết hơn nữa được không ạ? Rất vui khi được bạn giúp![]()
ABC cân vì có AB = AC
OAD đều vì nó là tổng 3 tam giác cân cộng lại.
 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
 trình bày rõ ràng chi tiết nhất ko làm tắt ạ e cảm ơn và kèm lói giải thích cụ thể
trình bày rõ ràng chi tiết nhất ko làm tắt ạ e cảm ơn và kèm lói giải thích cụ thể
a: Xét ΔMQP có
H,I lần lượt là trung điểm của MQ,MP
=>HI là đường trung bình của ΔMQP
=>HI//QP và HI=QP/2
Xét ΔPMN có
I,K lần lượt là trung điểm của PM,PN
=>IK là đường trung bình của ΔPMN
=>IK//MN và \(IK=\dfrac{MN}{2}\)
b: H,I,K thẳng hàng
mà HI//PQ và IK//MN
nên HI//MN
Ta có: HI//MN
HI//PQ
Do đó: MN//PQ
mn giải giúp mik vs ạ, giải chi tiết ra luôn, mình phải nộp trong hôm nay rùi ạ, cảm ơn mn nhìu


Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)
Giải gấp siêu gấp ạ . Giải rõ ràng bài này giúp mình trước 8 giờ hoặc sau 8 rưỡi . Mình hứa sẽ tích và chân thành cảm ơn . Nhưng phải giải rõ ràng và bằng cách lớp 4 ạ .
Hiện nay tổng số tuổi của hai bố con là 45 tuổi , biết 1 / 2 tuổi con bằng 1 / 7 tuổi bố . Hỏi hiện nay con bao nhiêu tuổi ?
Dễ lắm em
1/2 tuổi con =1/7 tuổi bố suy ra tuổi bống là 7 phần bằng nhau thì con chiếm hai phần
Phải vẽ sơ đồ đấy
Theo sơ đồ ,tổng số phần bằng nhau là:
2+7=9 (phần)
Tuổi bố là:
45:9*7=35(tuổi)
Tuổi con là:
45-35=10 (tuổi)
Đ/S:Tuổi bố: 35 tuổi
Tuổi con: 10 tuổi
Vì 1/2 tuổi con bằng 1/7 tuổi bố
=) Coi tuổi con là 2 phần bằng nhau thì tuổi bố là 7 phần như thế
Tổng số phần bằng nhau là: 2 + 7 = 9 (phần)
Giá trị của 1 phần là: 45 : 9 = 5 (tuổi)
Tuổi con hiện nay là: 5 x 2 = 10 (tuổi)
Kết quả đúng nhé bạn! k cho mik nhé! :)))
Chịu rồi, mik ko bít làm kểu lớp 4
e/ 2x = 3y = 5z và x –y + z = -33
giúp mình, giải thích rõ ràng ạ :))
\(2x=3y=5z\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x-y+z}{15-10+6}=\dfrac{-33}{11}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).15=-45\\y=\left(-3\right).10=-30\\z=\left(-3\right).6=-18\end{matrix}\right.\)
Theo tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{5}}=\dfrac{x-y+z}{\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{5}}=\dfrac{-33}{\dfrac{11}{30}}=-90\)
Do đó: x=-45; y=-30; z=-18
e/ 2x=3y=5z và x-y+z=-33
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
x/5=y/2=z/3 = x-y+z/5-2+3= -33/6= -11/2
Suy ra:
x/5= -11/2 => x=5.(-11/2)= -27,5
y/2= -11/2 => y=2.(-11/2)= -11
z/3= -11/2 => z=3.(-11/2)=-16,5
Đó nha, đáp án thì mik tính lại đúng rồi nhưng bạn trình bày theo mik hay của bạn thì tùy nhé^^
Mong là được giải trước 9h sáng ạ!!! Mình hứa tick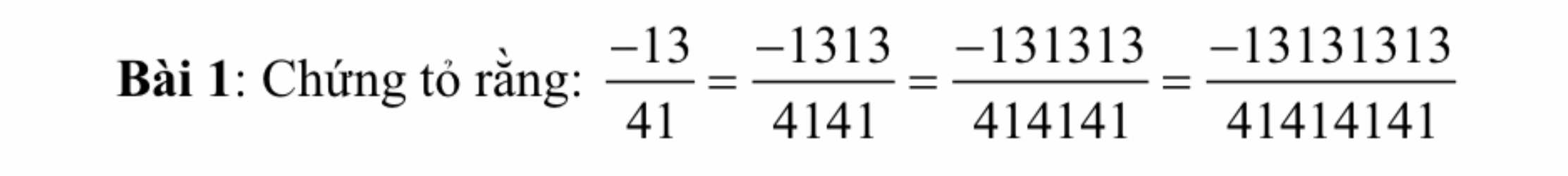
\(-\dfrac{13}{41}=\dfrac{-13.101}{41.101}=\dfrac{-1313}{4141}\) (1)
\(\dfrac{-13}{41}=\dfrac{-13.10101}{41.10101}=\dfrac{-131313}{414141}\)(2)
\(\dfrac{-13}{41}=\dfrac{-13.1010101}{41.1010101}=\dfrac{-13131313}{41414141}\)(3)
từ (1)(2)(3)=> \(\dfrac{-13}{41}=\dfrac{-1313}{4141}=\dfrac{-131313}{414141}=\dfrac{-13131313}{41414141}\)
Giải rõ ràng chi tiết hộ mk ạ
Giải chi tiết, rõ ràng hộ mk ạ
Cái này hầu như cơ bản nhiều ít nâng cao bạn chú ý vận dụng câu nào không hiểu hãy đăng để các bạn làm giải thích , chứ có mấy cái cơ bản làm rồi giải thích tốn thời gian lắm và không hiệu quả đối bạn đâu!