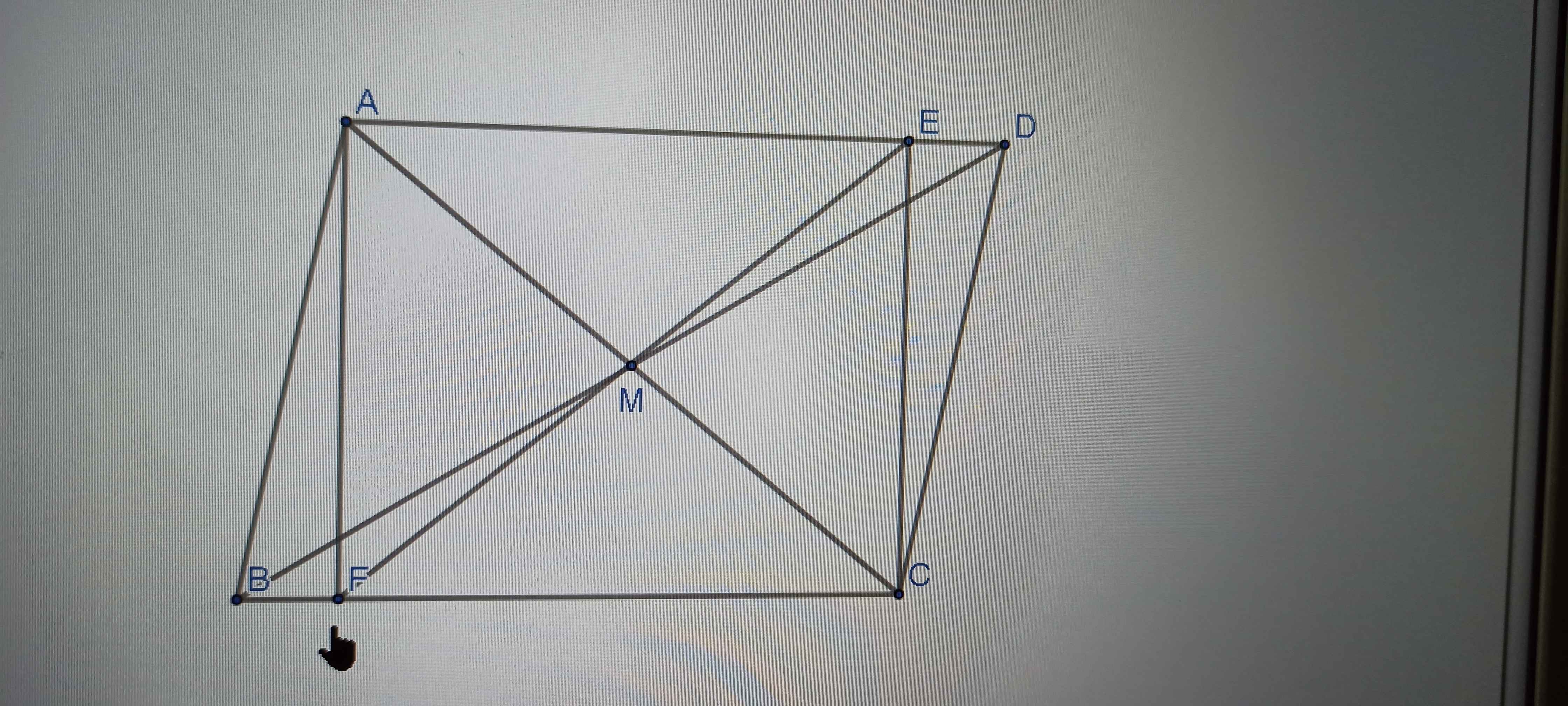
Cho tam giác ABC. Gọi M là trung điểm AC trên tia đối MB lấy D sao cho MB = MD a, AD // BC và AD = BC ? b, Lấy E là trung điểm AD ,nối EM cắt BC tại F chứng minh F là trung điểm BC c, Nếu MB= 1/2 AC . Hãy chứng minh góc BAD = 1 vuông

Những câu hỏi liên quan
cho tam giác ABC . gọi M là trung điểm cũa AC trên tia đối của tia MB , lấy điểm d sao cho MB = MD : chứng minh
AD = BC ; AD // BC
vẽ hình nx
Cho tam giác ABC, M là trung điểm của AC. Trên tia đối của MB lấy điểm D sao cho MB=MD, trên tia đối của tia BC lấy điểm E sao cho BE=BC. Gọi Y là giao điểm của của AB và DE. CMR Y là td của AD
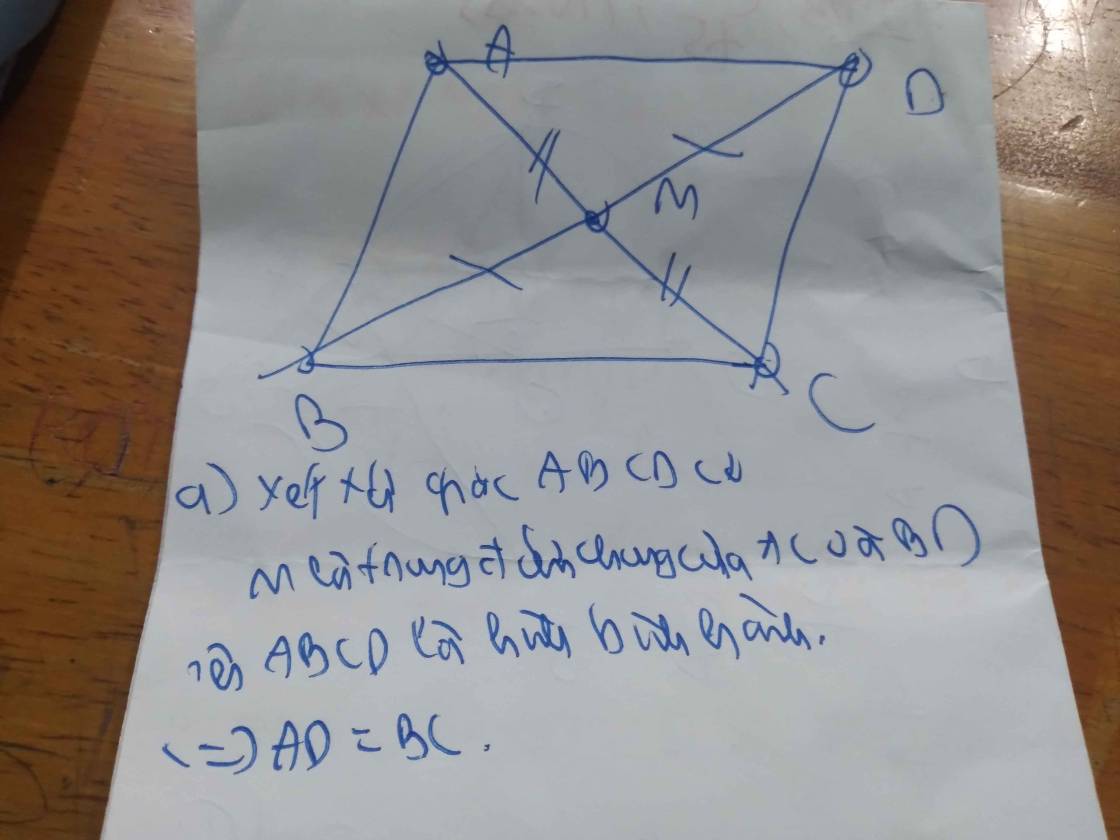
Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó:ABCD là hình bình hành
Suy ra: AD//BC và AD=BC
Xét tứ giác AEBD có
AD//BE
AD=BE
Do đó: AEBD là hình bình hành
Suy ra: Hai đường chéo AB và ED cắt nhau tại trung điểm của mỗi đường
hay Y là trung điểm của ED
Đúng 1
Bình luận (0)
Cho tam giác ABC gọi M là trưng điểm của AC trên tia đối tia MB lấy điểm D sao cho MD=MB
A, Chứng Minh AD=BC
Cho tam giác ABC, M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho MB=MD. Trên tia đối của tia BC lấy điểm E sao cho BE=BC. Gọi I là giao điểm của AB và BC. C/m
a) AD // BC
b)IA=IB
giúp mk với
Bạn ơi, sao I lại là giao điểm của AB và BC được?
Đúng 0
Bình luận (0)
Nối A với D
Xét Δ ADM và Δ CBM, ta có:
MD = MB (GT)
\(\widehat{AMD}\) = \(\widebat{CMB}\) (2 góc đối đỉnh)
AM = CM (vì M là trung điểm của AC)
=> Δ ADM = Δ CBM (c.g.c)
=> DA = BC (2 cạnh tương ứng) (1)
=> \(\widehat{ADM}\) = \(\widehat{CBM}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong tạo bởi đoạn thẳng BD cắt 2 đoạn thẳng CB và DA
=> AD // BC
hay AD // BE
=> \(\widehat{BAD}\) = \(\widehat{ABE}\) (2 góc so le trong)
hay \(\widehat{IAD}\) = \(\widehat{IBE}\) (1)
=> ADE = BED (2 góc so le trong)
hay \(\widehat{ADI}\) = \(\widehat{BEI}\) (2)
Ta có: BE = BC (GT)
Lại có: DA = BC (chứng minh trên)
=> DA = BE (3)
Xét Δ IAD và Δ IBE, ta có:
\(\widehat{IAD}\) = \(\widehat{IBE}\) (chứng minh trên)
DA = BE (chứng minh trên)
ADI = BEI (chứng minh trên)
=> Δ IAD = Δ IBE (g.c.g)
=> IA = IB (2 cạnh tương ứng)
Vậy IA = IB.
Lớp 8 r quên hết cách trình bày ^-^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC. M,N lần lượt là trung điểm của AC và AB. Trren tia đối MB lấy D sao cho MD=MB. Trên tia đối NC lấy E sao cho NE=NC. Chứng minh:a) tam giác AEN= tam giác BCN. b) tam giác AMD= tam giác CMB. c) AE=AD. d)AD// BC ; AE//BC
cho tam giác ABC. M là trung điểm của AC. Trên tia đối của MB lấy điểm D sao cho MD=MB a) chứng minh rằng AB=CD; BC=AD b) lấy I thuộc AD tia AD cắt BC ở K. Chứng minh MI= MK
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB=CD; AD=BC
b: Xet ΔAMI và ΔCMK có
\(\widehat{AMI}=\widehat{CMK}\)
MA=MC
\(\widehat{MAI}=\widehat{MCK}\)
Do đó: ΔAMI=ΔCMK
Suy ra: MI=MK
Đúng 0
Bình luận (0)
Gỉai nhanh giúp mình nehs . Thanks
Cho tam giác ABC vuông tại A . Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD =MB .Chứng mInh AD = BC
Cho tam giác ABC vuông tại A. Gọi M và N lần lượt là trung điểm của các cạnh AC và AB. Trên tia đối của tia
MB lấy điểm D sao cho MD = MB.
1. Chứng minh ∆AMB = ∆CMD và CDAC.
2. Chứng minh AD = BC và AD // BC.
3. Trên tia đối của tia NC lấy điểm E sao cho NE = NC, chứng minh A là trung điểm của ED.
Bài này bạn tự kẻ hình giúp mình nha!
1. Xét tam giác AMB và tam giác CMD có:
AM = CM ( M là trung điểm của AC )
AMB = CMD ( 2 góc đối đỉnh )
BM = DM (gt)
=> tam giác AMB = tam giác CMD (c.g.c) (dpcm)
=> BAM = DCM ( 2 góc tương ứng)
=> DCM = 90o => DC vuông góc với MC hay CD vuông góc với AC ( dpcm )
2.
Xét tam giác AMD và tam giác CMB có:
AM = CM ( Theo 1.)
AMD = CMB ( 2 góc đối đỉnh )
DM = BM (gt)
=> tam giác AMD = tam giác CMB ( c.g.c)
=> AD = BC (2 cạnh tương ứng) (dpcm)
=> ADM = CBM (2 góc tương ứng)
Mà góc ADM và và góc CBM ở vị trí so le trong
=> AD // BC (dpcm)
3. Xét tam giác AEN và tam giác BCN có:
AN=BN ( N là trung điểm của AB)
ANE = BNC ( 2 góc đối đỉnh )
NE = NC (gt)
=> Tam giác AEN = tam giác BCN ( c.g.c)
=> AE = BC ( 2 cạnh tương ứng ) (1)
=> EAN = CBN ( 2 góc tương ứng ) mà EAN và CBN ở vị trí so le trong => AE // BC (2)
Theo 2. ta có : +) AD=BC (3)
+) AD // BC (4)
Từ (1) và (3) Suy ra AE = AD (5)
Từ (2) và (4) Suy ra A,E,D thẳng hàng (6)
Từ (5) và (6) Suy ra A là trung điểm của ED (dpcm)
sorry bn nha
mk lm xong rùi
Cho tam giác ABC nhọn, M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho MD = MB. Chứng minh:
a) tam giác MAB = tam giác MCD và AB // CD
b) góc ABC = góc CDA
c) Kẻ CE vuông góc với AD tại E. Gọi F là điểm trên cạnh BC sao cho BF = DE. Chứng minh À vuông góc với BC và 3 điểm F, M, E thẳng hàng
Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.
Đúng 0
Bình luận (0)