Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a,SA=2a và S A ⊥ ( A B C ) . Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Tính 50 V 3 a 3 , với là thể tích khối chóp A.BCNM.
A. 10
B. 12
C. 9
D. 11
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a và (SAB) ^ (ABC); SA = a; S A B ^ = 60 ° . Tính thể tích V của S.ABC
A. V = a 3 3 8
B. V = a 3 3 12
C. V = a 3 3 6
D. V = a 3 2
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, S A ⊥ ( A B C ) và S A = a 6 . Thể tích của khối chóp S.ABC bằng:
A. a 3 2 4
B. a 3 2
C. a 3 3 12
D. a 3 2 12
Đáp án A
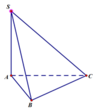
Do tam giác ABC đều cạnh a nên có S ∆ A B C = a 2 3 4
⇒ V = 1 3 S A . S ∆ A B C = 1 3 . a 6 . a 2 3 4 = a 2 2 4
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, A B = a , A C = 2 a , cạnh bên SA vuông góc với mặt đáy và SA=a. Tính thể tích V của khối chóp S.ABC .
A. V = a 3 2
B. V = a 3
C. V = a 3 4
D. V = a 3 3
Đáp án là D.
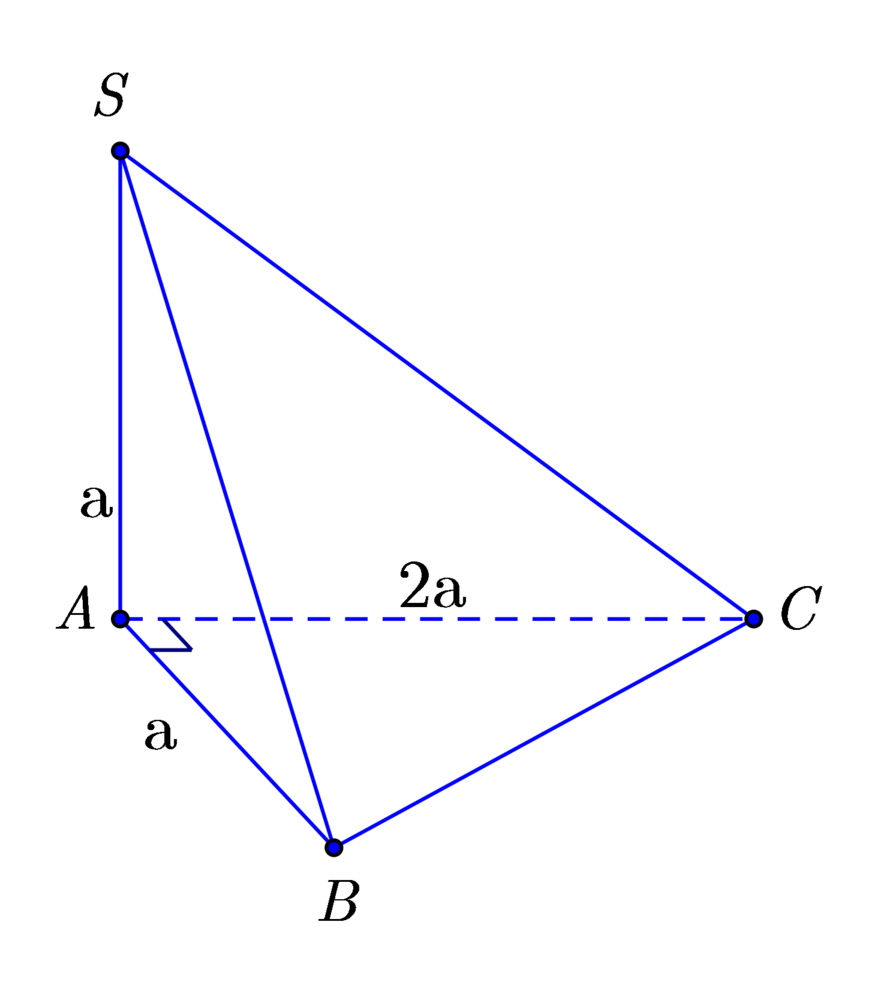
Ta có: V S . A B C = 1 6 A B . A C . S A = a 3 3 .
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, AB=a, AC=2a, cạnh bên SA vuông góc với mặt đáy và SA=a. Tính thể tích V của khối chóp S.ABC .
![]()
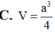
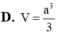
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy và SA = 2a. Tính thể tích khối chóp S.ABC
A. a 3 3 3
B. a 3 3 2
C. a 3 3 12
D. a 3 3 6
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Tính thể tích khối chóp S.ABC.
A. a 3 3 12
B. a 3 4
C. a 3 3 4
D. a 3 12
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Tính thể tích khối chóp S.ABC
A. V = a 3 3 12
B. V = a 3 4
C. V = a 3 3 4
D. V = a 3 12
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a 6 . Thể tích của khối chóp bằng:
A . a 3 2 4
B . a 3 2
C . a 3 3 12
D . a 3 2 12
Đáp án A
Do tam giác ABC đều cạnh a nên có 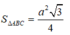
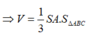

Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA ⊥ (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Tính 50 V 3 a 3 , với V là thể tích khối chóp A.BCMN
A. 10
B. 12
C. 9
D. 11
Phương pháp:
Tính thể tích V S . A B C
Tính thể tích V S . A M N theo công thức tỉ lệ thể tích
Tính thể tích V A . B C M N và suy ra kết luận
Cách giải:
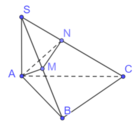
Xét tam giác SAB và SAC là các tam giác vuông tại A có hai cạnh góc vuông là a và 2a nên
![]()
Tam giác SAB vuông tại có đường cao AM
Khi đó ![]()
Tương tự ![]()
Lại có ![]()
Mặt khác 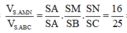
![]()
Do đó ![]()
![]()
Chọn C.