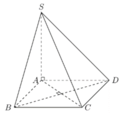
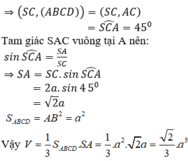Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng A B C D v à S A = a 6 . Gọi a là góc giữa đường thẳng SB và mặt phẳng (SAC). Tính sin α ta được kết quả là:
A. 1 14
B. 2 2
C. 3 2
D. 1 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và S A = a 6 . Tính thể tích V của khối chóp S.ABCD
A. V = a 3 6
B. V = a 3 6 4
C. V = a 3 6 6
D. V = a 3 6 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và S A = 6 Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 6 6
B. V = a 3 6 4
C. V = a 3 6 3
D. V = a 3 6
Đáp án C
V S . A B C D = 1 3 S . A . d t A B C D = 1 3 a 6 . a 2 = a 3 6 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và S A = a 6 Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 6 6
B. V = a 3 6 4
C. V = a 3 6 3
D. V = a 3 6
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và S A = a 6 . Tính thể tích V của khối chóp S.ABCD.
![]()
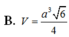
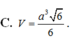
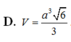
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SO tạo với mặt phẳng đáy một góc 450. Tính thể tích V của khối chóp S.ABCD.
A. a 3 2 2
B. a 3 2 3
C. a 3 2 6
D. a 3 2
Đáp án C
Ta có tam giác SAO vuông cân tạiA.
Suy ra:
S
A
=
O
A
=
A
C
2
=
a
2
2
Vậy : V S . A B C D = 1 3 . S O . S A B C D = a 3 2 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SO tạo với mặt phẳng đáy một góc 450. Tính thể tích V của khối chóp S.ABCD
A. V = a 3 2 2
B. V = a 3 2 3
C. V = a 3 2 6
D. V = a 3 2
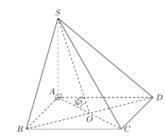
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA = 2a. Gọi B’, D’ lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SD. Mặt phẳng (AB’D’) cắt cạnh SC tại C’. Tính thể tích của khối chóp S.AB’C’D’.
A. a 3 3
B. 16 a 3 45
C. a 3 2
D. a 3 2 2
Đáp án B.
Gọi O là tâm của hình vuông ABCD, nối S O ∩ B ' D ' = I .
Và nối AI cát SC tại C’ suy ra mp (AB’D’) cắt SC tại C’.
Tam giác SAC vuông tại A, có S C 2 = S A 2 + A C 2 = 6 a 2 ⇒ S C = a 6 .
Ta có B C ⊥ S A B ⇒ B C ⊥ A B ' và S B ⊥ A B ' ⇒ A B ' ⊥ S C .
Tương tự A D ' ⊥ S C suy ra S C ⊥ ( A B ' D ' ) ≡ ( A B ' C ' D ' ) ⇒ S C ⊥ A C ' .
Mà S C ' . S C = S A 2 ⇒ S C ' S C = S A 2 S C 2 = 2 3 và S B ' S B = S A 2 S B 2 = 4 5 .
Do đó V S . A B ' C ' = 8 15 V S . A B C = 8 30 V S . A B C D mà V S . A B C D = 1 3 . S A . S A B C D = 2 a 3 3 .
Vậy thể tích cần tính là V S . A B ' C ' D ' = 2 . V S . A B ' C ' = 16 a 3 45
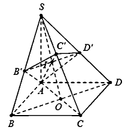
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = a. Khi đó, thể tích của khối chóp S.ABCD là:
A. a3/4
B. a3/3
C. a3
D. a3/2
Đáp án B
Thể tích của khối chóp S.ABCD là V = 1 3 S A . S A B C D = a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết thể tích của khối chóp S.ABCD theo a là V = 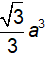
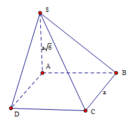
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45° và SC = 2a. Tính thể tích V của khối chóp S.ABCD.

Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).