Gieo một con súc sắc. Xác suất để mặt chẵn chấm xuất hiện là:
A. 0,5
B. 0,3
C. 0,2
D. 0,4
Những câu hỏi liên quan
Gieo một con súc sắc. Xác suất để mặt chẵn chấm xuất hiện là:
A. 0,5.
B. 0,3.
C. 0,2.
D. 0,4.
Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
Đọc tiếp
Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là A. 1 B.
1
3
C.
2
3
D.
1
2
Đọc tiếp
Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
A. 1
B. 1 3
C. 2 3
D. 1 2
Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là:
A . 1
B . 1 2
C . 1 3
D . 2 3
Chọn B
Không gian mẫu là: 
Gọi A là biến cố: “Mặt có số chấm chẵn xuất hiện”.
Xác suất để mặt có số chấm chẵn xuất hiện là:
Đúng 0
Bình luận (0)
Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất để xuất hiện mặt chẵn chấm?
A
.
1
6
B
.
1
4
C
.
1
2
D
.
1
3
Đọc tiếp
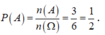
Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất để xuất hiện mặt chẵn chấm?
A . 1 6
B . 1 4
C . 1 2
D . 1 3
Chọn C
Gọi A là biến cố “ Súc sắc xuất hiện mặt chẵn chấm”
Đúng 0
Bình luận (0)
Gieo đồng thời hai con súc sắc. Xác suất để số chấm trên mặt xuất hiện của cả hai con súc sắc đều là số chẵn bằng A.
1
4
B.
1
12
C.
1
36
D.
1
6
Đọc tiếp
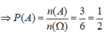
Gieo đồng thời hai con súc sắc. Xác suất để số chấm trên mặt xuất hiện của cả hai con súc sắc đều là số chẵn bằng
A. 1 4
B. 1 12
C. 1 36
D. 1 6
Đáp án là A.
• Số phần tử không gian mẫu n ( Ω ) = 36
• Gọi biến cố A: " Số chấm xuất hiện trên mặt của hai con súc sắc là số chẳn".
Ta có các khả năng xảy ra:
Đúng 0
Bình luận (0)
Gieo đồng thời hai con súc sắc. Xác suất để số chấm trên mặt xuất hiện của cả hai con súc sắc đều là số chẵn bằng A.
1
4
B.
1
12
C.
1
36
D.
1
6
Đọc tiếp
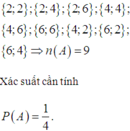
Gieo đồng thời hai con súc sắc. Xác suất để số chấm trên mặt xuất hiện của cả hai con súc sắc đều là số chẵn bằng
A. 1 4
B. 1 12
C. 1 36
D. 1 6
Đáp án là A
Số phần tử không gian mẫu n Ω = 36
Gọi biến cố " Số chấm xuất hiện trên mặt của hai con súc sắc là số chẳn".
Ta có các khả năng xảy ra:
2 ; 2 ; 2 ; 4 ; 2 ; 6 ; 4 ; 4 ; 4 ; 6 ; 6 ; 6 ; 4 ; 2 ; 6 ; 2 ; 6 ; 4 ⇒ n A = 9
Xác suất cần tính: P A = 1 4
Đúng 0
Bình luận (0)
Gieo đồng thời hai con súc sắc. Tính xác suất sao cho:
a. Hai con súc sắc đều xuất hiện mặt chẵn.
b. Tích các số chấm trên hai con súc sắc là số lẻ.
Không gian mẫu là kết quả của việc gieo đồng thời hai con xúc sắc.
⇒ Ω = {(i; j); 1 ≤ i, j ≤ 6}.
⇒ n(Ω) = 6.6 = 36.
a) Gọi A: “Cả hai con xúc sắc đều xuất hiện mặt chẵn”
⇒ A = {(2; 2); (2; 4); (2; 6); (4; 2); (4; 4); (4; 6); (6; 2); (6; 4); (6; 6)}
⇒ n(A) = 9.
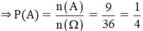
b) Gọi B: “Tích số chấm trên hai con xúc sắc là số lẻ”
Vì tích hai số là lẻ chỉ khi cả hai thừa số đều lẻ nên :
B = {(1; 1); (1; 3); (1; 5); (3; 1); (3; 3); (3; 5); (5; 1); (5; 3); (5; 5)}
⇒ n(B) = 9
Đúng 0
Bình luận (0)
Gieo một đồng tiền, sau đó gieo một con súc sắc. Quan sát sự xuất hiện mặt sấp (S), mặt ngửa (N) của đồng tiền và số chấm xuất hiện trên con súc sắc.a) Xây dựng không gian mẫu.b) Xác định các biến cố sau:A. Đồng tiền xuất hiện mặt sấp và con súc sắc xuất hiện mặt chấm chẵn;B. Đồng tiền xuất hiện mặt ngửa và con súc sắc xuất hiện mặt lẻ chấm;
Đọc tiếp
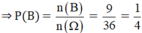
Gieo một đồng tiền, sau đó gieo một con súc sắc. Quan sát sự xuất hiện mặt sấp (S), mặt ngửa (N) của đồng tiền và số chấm xuất hiện trên con súc sắc.
a) Xây dựng không gian mẫu.
b) Xác định các biến cố sau:
A. "Đồng tiền xuất hiện mặt sấp và con súc sắc xuất hiện mặt chấm chẵn";
B. "Đồng tiền xuất hiện mặt ngửa và con súc sắc xuất hiện mặt lẻ chấm";
a) Ω = {S1, S2, S3, S4, S5, N1, N2, N3, N4, N5}
b)
A = {S2, S4, S6};
B = {N1, N3, N5}.
Đúng 0
Bình luận (0)