Đồ thị của hàm số y = (-2)/5x là đường thẳng OM. Khi đó:
(A) M(-5; 2)
(B) M(2; -5)
(C) M((-2)/5; 1)
(D) M((-6)/5; 3)
Cho đồ thị hàm số y = ax (a ≠ 0) là đường thẳng OM trên hình vẽ. Khi đó hệ số a bằng
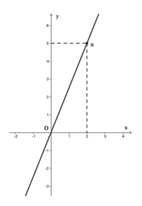
A. 5
B. 5/2
C. 2/5
D. 1
Từ đồ thị hàm số ta thấy điểm M(2, 5) thuộc đồ thị hàm số nên ta thay x = 2, y = 5 vào hàm số y = ax (a ≠ 0) ta được 5 = a.2 ⇒ a = 5/2 (TM)
Vậy a = 5/2
Chọn đáp án B
Cho đồ thị hàm số y = ax (a ≠ 0) là đường thẳng OM trên hình vẽ. Khi đó hệ số a bằng
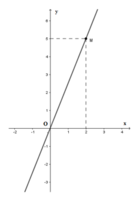
A. 5
B. 5/2
C. 2/5
D. 1
Từ đồ thị hàm số ta thấy điểm M(2, 5) thuộc đồ thị hàm số nên ta thay x = 2; y = 5 vào hàm số y = ax (a ≠ 0) ta được 5 = a.2 ⇒ a = 5/2 (TM)
Vậy a = 5/2
Chọn đáp án B
Cho đồ thị hàm số y = ax ( a ≠ 0 ) là đường thẳng OM trên hình vẽ . Khi đó hệ số a bằng
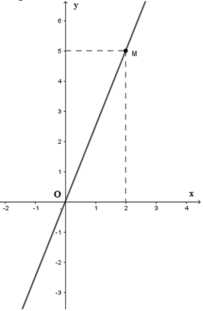
A. 5
B. 5 2
C. 2 5
D. 1
Từ đồ thị hàm số ta thấy điểm M(2;5)thuộc đồ thị hàm số nên ta thay x = 2; y = 5 vào hàm số y = ax ( a ≠ 0 ), được: 5= a.2 => a = 5 2 (TM)
Vậy a = 5 2
Đáp án cần chọn là: B
Cho hàm số bậc nhất y = (2m – 1)x + m – 1, với m là tham số.
a) Khi m = 2, vẽ đồ thị của hàm số thu được và tính diện tích tam giác tạo bởi đồ thị và hai trục toạ độ. Gọi đường thẳng đó là (d1)
b) Khi m = - 1, vẽ đồ thị là đường thẳng (d2) của hàm số. Tính khoảng cách từ gốc toạ độ O đến đường thẳng (d2).
c) Chứng minh rằng khi m thay đổi thì các đường thẳng thu được luôn cùng đi qua
một điểm cố định.
1. Cho hai hàm số bậc nhất y=mx+3 và y=(2m+1)x – 1.
Để đồ thị của hai hàm số đã cho là hai đường thẳng song song với nhau thì m = …
2. Cho hàm số y = ax+3. Để đồ thị hàm số song song với đường thẳng y = -5x thì a = …
\(1,\Leftrightarrow m=2m+1\Leftrightarrow m=-1\\ 2,\Leftrightarrow a=-5\)
a,vẽ đồ thị hàm số trên khi m=3
b,tìm m để đường thẳng d song song với đường thẳng d1 : y=2x+5
c, đường thẳng d cắt trục Ox tại điểm A , cắt trục Oy tại điểm B . tìm giá trị của m để diện tích tam giác AOB bằng 1 đơn vị diện tích
b: Để hai đường song song thì m-2=2
=>m=4
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\x=\dfrac{-2}{m-2}\end{matrix}\right.\Leftrightarrow OA=\dfrac{2}{\left|m-2\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Leftrightarrow OB=2\)
SAOB=1
=>1/2*4/|m-2|=1
=>4/|m-2|=2
=>|m-2|=2
=>m=4 hoặc m=0
Cho hàm số bậc nhất \(y=\left(2m-1\right)x-3m+5\) có đồ thị hàm số là đường thẳng (d)
a) Vẽ đồ thị hàm số khi m = 2
b) Tìm m để (d) song song với đường thẳng (\(d_1\)) : \(y=-3x+2\)
c) Tìm m để (d) cắt đường thẳng (\(d_1\)) : \(y=-3x+2\) tại 1 điểm nằm trên trục tung
a) Khi m =2 thì y = 3x - 1
(Bạn tự vẽ tiếp)
b) Để \((d)//(d_{1})\) thì \(\begin{cases} 2m-1=-3\\ -3m+5\neq2 \end{cases} \) ⇔ \(\begin{cases} m=-1\\ m\neq1 \end{cases} \) ⇔ \(m=-1\)
c)
Để \((d) ⋂ (d1)\) thì \(2m-1\neq-3 \) ⇔ \(m\neq-1\)
Giao điểm của 2 đường thẳng thuộc trục tung => x=0
Khi đó, ta có: \(y=-3.0+2=2\)
⇒ Điểm \((0;2)\) cũng thuộc đường thẳng (d)
⇒ \(2=(2m-1).0-3m+5\) ⇔ \(m=1\) (TM)
Cho hàm số y = ax-1. Tính hệ số góc của hàm số biết
a) Đồ thị hàm số vuông góc với đường thẳng y = 2x+3
b) Đồ thị hàm số song song với đường thẳng y = -5x+7
c) Đồ thị hàm số trùng với đường thẳng y = 5x-1
a.tìm m để đồ thị hàm số y=(2m-1)x-m+2 vuông góc với đường thẳng y=-x
b.cho đường thẳng d có pt:ax+(2a-1)y+3=0
tìm a để đường thẳng d đi qua điểm M(1;-1). khi đó hãy tìm hệ số góc của đường thẳng d
c.cho đường thẳng d có pt:y=mx+2m-4.tìm m để đồ thị hàm số đi qua gốc tọa độ