Tính thể tích chóp SABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy.
A. a 3 3 2
B. a 3 3
C. a 3 3 3
D. a 3 3 6
Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là một tam giác đều và nằm trong một mặt phẳng vuông góc với đáy (ABCD). Tính thể tích khối chóp SABCD.
A. a 3 6
B. a 3 3 2
C. a 3 3 6
D. a 3 2
Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
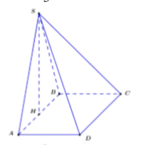
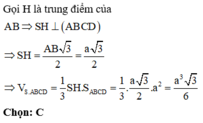
Cho hình chóp tứ giác SABCD có đáy là vuông; mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng ( SCD) bằng 3 7 a 7 . Tính thể tích Vcủa khối chóp SABCD
A. V = 1 3 a 3
B. V = a 3
C. V = 2 3 a 3
D. V = 3 a 3 2
Đáp án D
Gọi H,M lần lượt là trung điểm của AB và CD
Vì Δ S A B đều và mặt phẳng S A B ⊥ A B C D ⇒ S H ⊥ A B C D .
Ta có
C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ S H M (1)
Gọi I là hình chiếu vuông góc của H lên mặt phẳng S C D (2)
Từ (1) và (2) suy ra H I ⊥ S C D
Vì A B // C D ⇒ A B // S C D ⇒ d A , S C D = d H , S C D = H I = 3 a 7 7
Giải sử A B = x x > 0 ⇒ S H = x 3 2 H M = x .
Mặt khác: 1 H I 2 = 1 H M 2 + 1 S H 2 ⇔ 7 9 a 2 = 1 x 2 + 4 3 x 2 ⇔ x 2 = 3 a 2 ⇒ x = 3 a
Thể tích: V S . A B C D = 1 3 S H . S A B C D = 1 3 . 3 a 2 .3 a 2 = 3 a 3 2 (đvtt)
Tính thể tích chóp S.ABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy.
A . a 3 3 2
B . a 3 3
C . a 3 3 3
D . a 3 3 6
Đáp án D
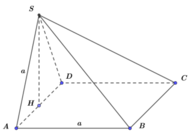
Ta có diện tích đáy S A B C D = a 2
Chiều cao SH = a 3 2
Từ đây ta tính được thể tích là: V S . A B C D = a 3 3 6
=> Chọn đáp án D
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp khối chóp SABCD.
A. 7 21 54 π a 3
B. 7 21 162 π a 3
C. 7 21 216 π a 3
D. 49 21 36 π a 3
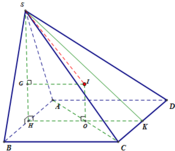
Gọi H là trung điểm của AB, suy ra A H ⊥ A B C D .
Gọi G là trọng tâm tam giác ∆SAB và O là tâm hình vuông ABCD.
Từ G kẻ GI//HO suy ra GI là trục đường tròn ngoại tiếp tam giác ∆SAB và từ O kẻ OI//SH thì OI là trục đường tròn ngoại tiếp hình vuông ABCD.
Ta có hai đường này cùng nằm trong mặt phẳng và cắt nhau tại I.
Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
R = S I = S G 2 + G I 2 = a 21 6 .
Suy ra thể tích khối cầu ngoại tiếp khối chóp S.ABCD là V = 4 3 π R 3 = 7 21 54 π a 3
Đáp án A
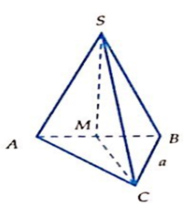
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a; mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông cân tại S. Tính thể tích V của khối chóp S.ABC.
A. V = a 3 3 12
B. V = a 3 3 24
C. V = a 3 3 6
D. V = a 3 3 8
cho hình chóp SABCD cạnh đáy a, đấy là hình vuông, tam giác SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy. Thể tích hình chóp là V. Tỉ số a³/V là
Cho hình chóp S.ABCD có đáy ABCD có đáy là hình vuông cạnh \(a\sqrt{2}\) . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy . Tính thể tích khối chóp S.ABCD ?
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(SH=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{1}{3}SH.AB^2=\dfrac{1}{3}.\dfrac{a\sqrt{6}}{2}.2a^2=\dfrac{a^3\sqrt{6}}{3}\)
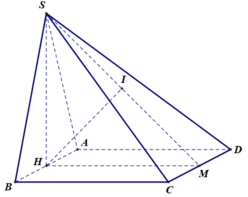
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 3 , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là:
A. 9 3 a 3 2
B. a 3 2
C. 3 a 3 3
D. 3 a 3 2
Chọn D.
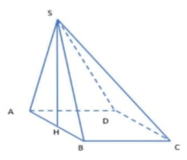
Ta có: SA=SB=AB=a 3
Gọi H là trung điểm của AB.
Do (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD). Khi đó SH= 3 a 2
Diện tích đáy S A B C D = 3 a 2
Vậy thể tích khối chóp
V
S
.
A
B
C
D
=
1
3
S
H
.
S
A
B
C
D
=
3
a
2
2
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp SABCD bằng
A. a 3 3 4
B. a 3 3 6
C. 5 a 3 3 6
D. 7 a 3 3 6