Trong không gian với hệ tọa độ Oxyz, cho u → = 1 ; − 2 ; 3 . Trong các vectơ sau, đâu là vectơ vuông góc với vectơ u → ?

A.  a → = 2 ; − 4 ; 6 .

B.  b → = 0 ; 3 ; − 2 .

C.  c → = − 1 ; 1 ; − 1 .

D.  d → = 2 ; 4 ; 2 .

Trong không gian với hệ tọa độ Oxyz, cho u → = ( 1 ; − 2 ; 3 ) . Trong các vectơ sau, đâu là vectơ vuông góc với vectơ u → ?

A.  a → = ( 2 ; − 4 ; 6 )

B.  b → = ( 0 ; 3 ; − 2 )

C.  c → = ( − 1 ; 1 ; − 1 )

D.  d → = ( 2 ; 4 ; 2 )

Trong không gian với hệ tọa độ Oxyz, cho  u → = (1;-2;3).

Trong các vectơ sau, đâu là vectơ vuông góc với vectơ u → ?

Trong không gian với hệ tọa độ Oxyz, cho u → = 2 j → - 4 i → + 6 k → . Tìm tọa độ của vectơ u → ?

Trong không gian với hệ tọa độ Oxyz ,cho hai vectơ  u → = ( 1 ; 2 ; 3 )  và  v → = ( - 5 ; 1 ; 1 )  . Khẳng định nào đúng?

A.  u → = v →   

B.  u → ⊥ v →  

C.  u → = v →  

D.  u → / / v →  

Trong không gian với hệ tọa độ Oxyz, cho hai vectơ  u → = 1 ; 2 ; 3   v à   v → = - 5 ; 1 ; 1 . Khẳng định nào đúng?

A.  u → = v →

B. u → ⊥ v →

C. u → = v →

D. u → / / v →

Trong không gian với hệ tọa độ O x y z , cho hai điểm A ( 1 ; 1 ; - 1 ) , B ( 2 ; 3 ; 2 ) . Vectơ  A B → có tọa độ là

A.  ( 1 ; 2 ; 3 )

B. ( - 1 ; - 2 ; 3 )

C. ( 3 ; 5 ; 1 )

D. ( 3 ; 4 ; 1 )

Trong không gian với hệ tọa độ Oxyz, cho vectơ u → = 2 ; - 1 ; 2  và vectơ v →  có độ dài bằng 1 thỏa mãn u → - v → = 4 . Độ dài của vectơ u → + v →  bằng 

A. 4

B. 3

C. 2

D. 1

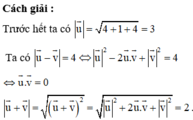
Trong không gian với hệ tọa độ Oxyz, biết  u → = 2 ;  v → = 1 ; và góc giữa hai vectơ  u →  và  v →  bằng  2 π 3  . Tìm k để vectơ  p → = k u → + v →  vuông góc với vectơ  q → = u → - v → .
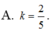