Tìm tất cả các giá trị thực của tham số a để biểu thức B = log 3 2 − a có nghĩa
A. a > 2
B. a = 3
C. a ≤ 2
D. x = 2
Tìm tất cả các giá trị thực của tham số a để biểu thức B = log 3 ( 2 - a ) có nghĩa
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 2 m x + 4 ) có tập xác định là ℝ .
A . - 2 ≤ m ≤ 2
B . m = 2
C . m > 2 h o ặ c m < - 2
D . - 2 < m < 2
Chọn D
y = log ( x 2 - 2 m x + 4 )
Điều kiện xác định của hàm số trên ![]()
Để tập xác định của hàm số là
ℝ
thì 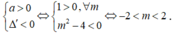
Vậy đáp án đúng là đáp án D.
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 2 m x + 4 ) có tập xác định là R
A. - 2 ≤ m ≤ 2
B. m = 2
![]()
D. -2 < m < 2
Tìm tất cả các giá trị thực của tham số m để y = l o g ( x 2 - 4 x - m + 1 ) có tập xác định là R
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y= log( x2- 2x- m+ 1) có tập xác định là R
A. m≥ 0.
B. m<0
C. m ≤ 2.
D. m> 2.
Chọn B
Để hàm số đã cho có tập xác định là R khi và chỉ khi : x2- 2x-m+ 1> 0 với mọi x
Hay
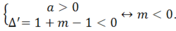
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là R
A. m > -4
B. m < 0
C. m < -4
D. m < -3
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là ℝ .
A. m > -4
B. m < 0
C. m < -4
D. m < -3
Chọn D
Hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là ℝ khi và chỉ khi
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 2 x - m + 1 ) có tập xác định là R:
A. m ≥ 0
B. m < 0
C. m ≤ 2
D. m > 2
Cho hai tập hợp A = [−2; 3) và B = [m; m+5). Tìm tất cả các giá trị thực của tham số m để A ∩ B ≠ ∅
A. − 7 < m ≤ − 2
B. − 2 < m ≤ 3
C. − 2 ≤ m < 3
D. - 7 < m < 3