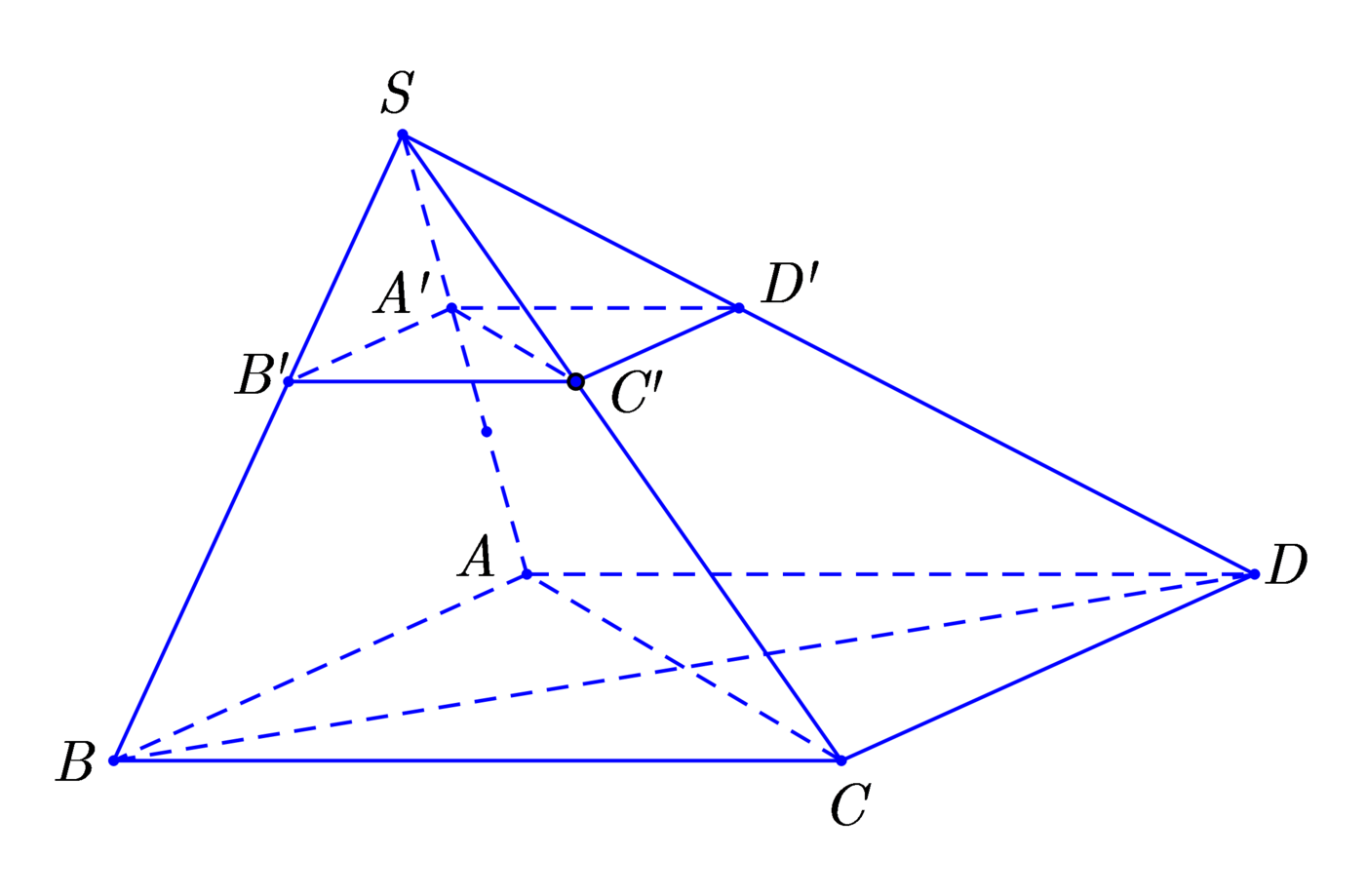
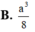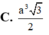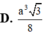Cho hình chóp S.ABCD có thể tích bằng 27 m 3 . Lấy A' trên SA sao cho S A = 3 S A ' . Mặt phẳng qua A' và song song với đáy hình chóp cắt SB, SC, SD lần lượt tại B’, C’, D’. Tính thể tích hình chóp S.A’B’C’D’
A. 3 m 3
B. 1 m 3
C. 5 m 3
D. 6 m 3
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3 B. V/9
C. V/27 D. V/81.
Cho hình chóp S.ABCD có thể tích bằng 27 m 3 Lấy A' trên SA sao cho SA=3SA' Mặt phẳng qua A' và song song với đáy hình chóp cắt SB, SC, SD lần lượt tại B’, C’, D’. Tính thể tích hình chóp S.A’B’C’D’
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy BACD là hình vuông cạnh a, cạnh bên SA = a và vuông góc với mặt đáy (ABCD). Trên SB, SD lần lượt lấy hai điểm M, N sao cho S M S B = m > 0 , S N S D = n > 0 . Tính thể tích lớn nhất V max của khối chóp S,AMN biết 2 m 2 + 3 n 2 = 1 .
A. V max = a 3 6 72
B. V max = a 3 48
C. V max = a 3 3 24
D. V max = a 3 6
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A ' trên cạnh SA sao cho S A ' = 1 3 S A . Mặt phẳng qua A ' và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lần lượt tại B ' C ' D ' . Tính theo V thể tích khối chóp S.A’B’C’D’ ?
A. V 3
B. V 81
C. V 27
D. V 9

Do
![]()
và S A ' = 1 3 S A nên

Chọn: C
Chú ý: Công thức tỉ số thể tích trên chỉ áp dụng cho hình chóp tam giác.
Cho hình chóp tứ giác S . A B C D có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho S A ' = 1 3 S A . Một mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh S B , S C , S D lần lượt tại B ' , C ' , D ' . Khi đó thể tích của khối chóp S . A ' B ' C ' D ' tính theo a bằng
A. V 3
B. V 9
C. V 27
D. V 81
Đáp án là C
V S . A ' B ' C ' V S . A B C = 1 27 ⇒ V S . A ' B ' C ' = 1 27 V S . A B C ⇒ V S . A B C D = 2 V S . A ' B ' C ' = 2 27 . 1 2 V S . A B C D = V 27 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Trên đường thẳng vuông góc với (ABCD) lấy điểm S' thỏa mãn S ' D = 1 2 S A và S, S’ ở cùng phía đối với mặt phẳng (ABCD). Gọi V 1 là thể tích phần chung của hai khối chóp S.ABCD và S’.ABCD . Gọi V 2 là thể tích khối chóp S.ABCD. Tỉ số V 1 V 2 bằng
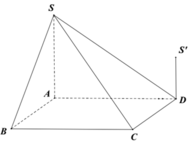
A. 7 18
B. 1 3
C. 7 9
D. 4 9
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Trên đường thẳng vuông góc với tại D lấy điểm S’ thỏa mãn S ' D = 1 2 S A và S, S’ ở cùng phía đối với mặt phẳng (ABCD). Gọi V 1 là thể tích phần chung của hai khối chóp S.ABCD và S’.ABCD. Gọi V 2 là thể tích khối chóp S.ABCD, tỉ số V 1 V 2 bằng
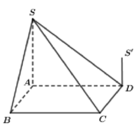
![]()
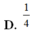
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Trên đường thẳng vuông góc với A B C D tại D lấy điểm S’ thỏa mãn S ' D = 1 2 S A và S, S’ ở cùng phía đối với mặt phẳng (ABCD). Gọi V 1 là thể tích phần chung của hai khối chóp S.ABCD và S’.ABCD. Gọi V 2 là thể tích khối chóp S.ABCD, tỉ số V 1 V 2 bằng
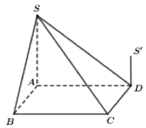
A. 1 2
B. 1 3
C. 2 2
D. 1 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh SA vuông góc với đáy và SA=y Trên cạnh AD lấy điểm M sao cho AM=x Biết rằng x 2 + y 2 = a 2 Tìm giá trị lớn nhất của thể tích khối chóp S.ABCM.