Cho hàm số y = f(x) có đồ thị hàm số y = f ' x như hình vẽ:
Xét hàm số g x = 2 f x + 2 x 3 − 4 x − 3 m − 6 5 với m là số thực. Điều kiện cần và đủ để g x ≤ 0 ∀ x ∈ − 5 ; 5 là:
A. m ≥ 2 3 f 5
B. m ≥ 2 3 f − 5
C. m ≥ 2 3 f 0
D. m ≤ 2 3 f 5
Những câu hỏi liên quan
Cho hàm số y f( x) . Hàm số y f’(x) có đồ thị như hình bên. Hàm số y g( x) f( 2-x) đồng biến trên khoảng A. (1; 3) B. ( 2; + ∞) C. ( -2;l ) D. ( -∞; -2)
Đọc tiếp
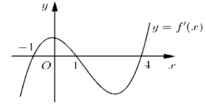
Cho hàm số y= f( x) . Hàm số y= f’(x) có đồ thị như hình bên. Hàm số y= g( x) = f( 2-x) đồng biến trên khoảng
A. (1; 3)
B. ( 2; + ∞)
C. ( -2;l )
D. ( -∞; -2)
Chọn C
+ Áp dụng công thức đạo hàm của hàm hợp ta có:
g’( x) = ( 2-x)’. f’( 2-x) = -f’( 2-x)
+ Nhận xét: Hàm số y= f( x) đã cho nghịch biến trên các khoảng (- ∞; -1) và ( 1;4) ( trên 2 khoảng đó f’(x) < 0) .
+ Hàm số đồng biến khi và chỉ khi
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm trên R. Đồ thị hàm số yf’(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x)-x-f(x) đạt cực đại tại? A. x -1 B. x 0 C. x 1 D. x 2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x)=-x-f(x) đạt cực đại tại?
A. x = -1
B. x = 0
C. x = 1
D. x = 2
Cho hàm số yf(x) có đạo hàm trên R. Đồ thị hàm số yf (x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x)f(x)-x có bao nhiêu điểm cực trị? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x)=f(x)-x có bao nhiêu điểm cực trị?
A. 1
B. 2
C. 3
D. 4
Cho hàm số y f(x) có đạo hàm f(x) trên khoảng
(
-
∞
;
+
∞
)
. Đồ thị hàm số y f(x) như hình vẽ Đồ thị của hàm số
y
(
f
(
x
)
)
2...
Đọc tiếp
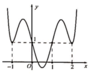
Cho hàm số y = f(x) có đạo hàm f'(x) trên khoảng
(
-
∞
;
+
∞
)
. Đồ thị hàm số y = f(x) như hình vẽ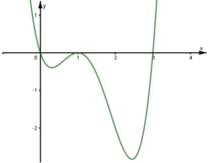 
Đồ thị của hàm số y = ( f ( x ) ) 2 có bao nhiêu điểm cực đại, cực tiểu?
A. 2 điểm cực đại, 3 điểm cực tiểu.
B. 1 điểm cực đại, 3 điểm cực tiểu.
C. 2 điểm cực đại, 2 điểm cực tiểu.
A. 3 điểm cực đại, 2 điểm cực tiểu.
Cho hàm số y f(x) . Biết f(x) có đạo hàm f’(x) và hàm số y f’(x) có đồ thị như hình vẽ. Hàm số g( x) f(x- 1) đạt cực đại tại điểm nào dưới đây? A. x 2 B. x 4 C . x 3 D. x 1
Đọc tiếp
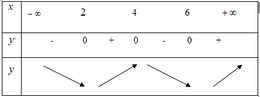
Cho hàm số y= f(x) . Biết f(x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ.
Hàm số g( x) = f(x- 1) đạt cực đại tại điểm nào dưới đây?
A. x= 2
B. x= 4
C . x= 3
D. x= 1
Chọn B
+ Dựa vào đồ thị hàm số ta thấy :
- Hàm số y= f( x) nghịch biến trên khoảng ( - ∞; 1) và ( 3; 5) .
- Hàm số y= f( x) nghịch biến trên khoảng ( 1 ; 3) và ( 5 ; + ∞)
Đúng 1
Bình luận (0)
Cho hàm số
y
f
(
x
)
có đạo hàm liên tục trên
ℝ
và có đồ thị hàm số
y
f
(
x
)
như hình vẽ. Đặt
g
(
x
)
f
(
x
3
)
. Tìm số điểm cực trị của hàm số
y
g
(
x...
Đọc tiếp
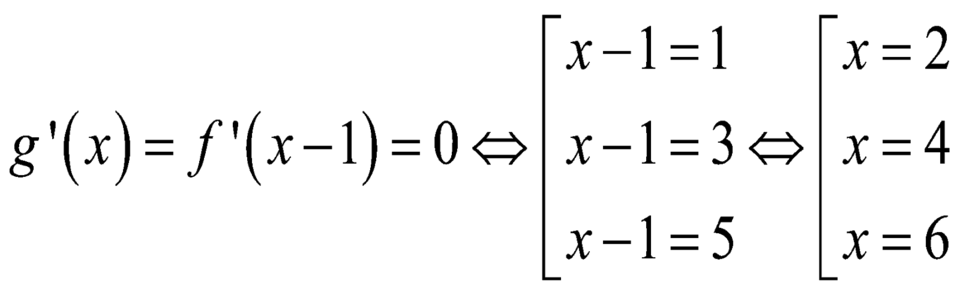
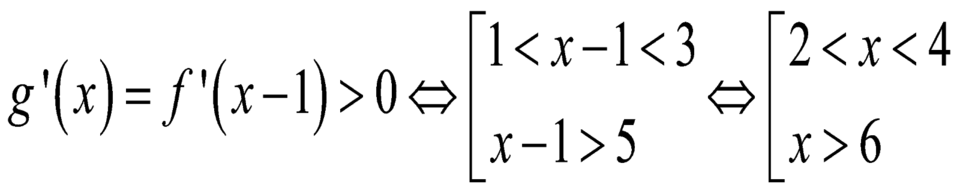
Cho hàm số y = f ( x ) có đạo hàm liên tục trên ℝ và có đồ thị hàm số y = f ' ( x ) như hình vẽ. Đặt g ( x ) = f ( x 3 ) . Tìm số điểm cực trị của hàm số y = g ( x )
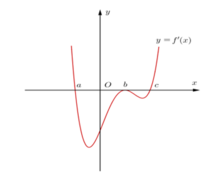
A. 3
B. 5
C. 4
D. 2
Cho hàm số y f(x) và y g(x) có đồ thị lần lượt như hình vẽĐồ thị hàm số y f(x).g(x) là đồ thị nào dưới đây?
Đọc tiếp
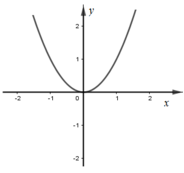
Cho hàm số y = f(x) và y = g(x) có đồ thị lần lượt như hình vẽ
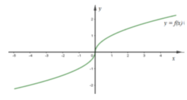
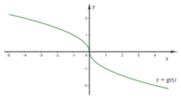
Đồ thị hàm số y = f(x).g(x) là đồ thị nào dưới đây?
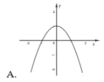
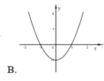
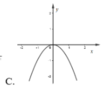
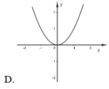
Đáp án C.
Cách giải:
Đặt y = f(x).g(x) = h(x). Khi đó:
h(0) = f(0).g(0) = 0.0 = 0
h(1) = f(1).g(1) = 1.(-1) = -1
Do đó, ta chọn phương án C
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm liên tục trên R đồ thị hàm số y f’(x) như hình vẽ.Biết f(2) –6, f(–4) –10 và hàm số g(x) f(x)+
x
2
2
, g(x) có ba điểm cực trị. Phương trình g(x) 0? A. Có đúng 2 nghiệm B. Vô nghiệm C. Có đúng 3 nghiệm D. Có đúng 4 nghiệm
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
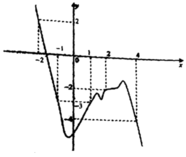
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Đáp án B
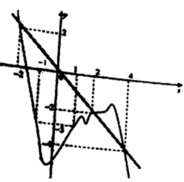
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: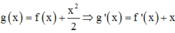 
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
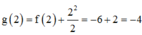
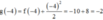
Bảng biến thiên:
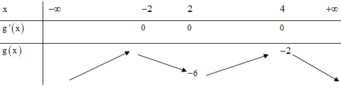
Dựa vào bảng biến thiên ta thấy 
=> phương trình g(x) = 0 không có nghiệm 
Đúng 0
Bình luận (0)
Cho hàm số yf(x) biết hàm số f(x)có đạo hàm f(x) và hàm số yf(x) có đồ thị như hình vẽ. Đặt g(x0f(x+1) Kết luận nào sau đây là đúng? A. Hàm số g(x) đồng biến trên khoảng (3;4) B. Hàm số g(x) đồng biến trên khoảng (0;1) C. Hàm số g(x) nghịch biến trên khoảng (4;6) D. Hàm số g(x) nghịch biến trên khoảng (
2
;
+
∞
)
Đọc tiếp
Cho hàm số y=f(x) biết hàm số f(x)có đạo hàm f'(x) và hàm số y=f'(x) có đồ thị như hình vẽ. Đặt g(x0=f(x+1) Kết luận nào sau đây là đúng?
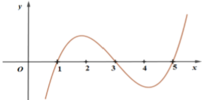
A. Hàm số g(x) đồng biến trên khoảng (3;4)
B. Hàm số g(x) đồng biến trên khoảng (0;1)
C. Hàm số g(x) nghịch biến trên khoảng (4;6)
D. Hàm số g(x) nghịch biến trên khoảng ( 2 ; + ∞ )
Cho hàm sốyf(x) có đạo hàm f(x) trên tập số thực
ℝ
và đồ thị của hàm số yf(x) như hình vẽ. Khi đó, đồ thị của hàm số
y
(
f
(
x
)
)
2
có A. 2 điểm cực đại, 2 điểm cực tiểu B. 2 điểm cực tiểu, 3 điểm cực đại C. 1 điểm cực đại, 3 điểm cực tiểu D. 2 điểm cực đại, 3 điểm cực tiểu
Đọc tiếp
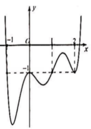
Cho hàm sốy=f(x) có đạo hàm f'(x) trên tập số thực ℝ và đồ thị của hàm số y=f(x) như hình vẽ. Khi đó, đồ thị của hàm số y = ( f ( x ) ) 2 có
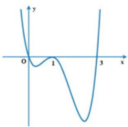
A. 2 điểm cực đại, 2 điểm cực tiểu
B. 2 điểm cực tiểu, 3 điểm cực đại
C. 1 điểm cực đại, 3 điểm cực tiểu
D. 2 điểm cực đại, 3 điểm cực tiểu
Từ đồ thị hàm số f(x) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ x=0;x=1;x=3
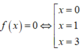
Lại thấy đồ thị hàm số y=f(x) có ba điểm cực trị nên
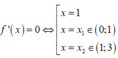
Hàm số y = f x 2 có đạo hàm y'=2f(x).f '(x)
Xét phương trình
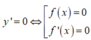
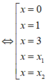
Ta có BXD của y' như sau
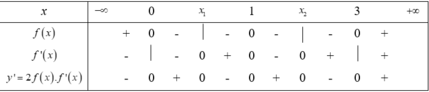
Nhận thấy hàm số y = f x 2 có y' đổi dấu từ âm sang dương tại ba điểm x=0;x=1;x=3 nên hàm số có ba điểm cực tiểu. Và y' đổi dấu từ dương sang âm tại hai điểm x = x 1 ; x = x 2 nên hàm số có hai điểm cực đại.
Chọn đáp án D.
Đúng 0
Bình luận (0)