Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [0;1], thỏa mãn  ( f ' ( x ) ) 2 + 4 f ( x ) = 8 x 2 + 4 , ∀ x ∈ [ 0 ; 1 ] và f(1) = 2. Tính  ∫ 0 1 f ( x ) d x

A .   1 3

B. 2.

C .   4 3

D .   21 4

Cho hàm số y = f ( x )  thỏa mãn f ( 2 ) = 1 4  và f ' ( x ) = 2 x . [ f ( x ) ] 2  với ∀ x ∈ R  tính f ( 1 )  

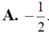
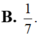
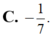
Cho hàm số y=f(x) có đạo hàm dương trên [1;2] thỏa mãn f ( 1 ) = 1 e và x f ' ( x ) + ( x + 1 ) f ( x ) = 3 x 2 e - x . Tính f(2)

A.   f ( 2 ) = 1 e 2

B.  f ( 2 ) = 2 e 2

C.  f ( 2 ) = 4 e 2

D.  f ( 2 ) = 8 e 2

Cho hàm số y=f(x) có đạo hàm liên tục trên ( 0 ; + ∞ ) thỏa mãn  f ' ( x ) + f ( x ) x = 4 x 2 + 3 x và f(1)=2. Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x = 2 là x

A. y =  16x+20. 

B. y = -16x+20 

C. y = -16x-20 

D. y = 16x-20.

Cho hàm số y=f(x) xác định, có đạo hàm trên R thỏa mãn  f 2 ( - x ) = ( x 2 + 2 x + 4 ) f ( x + 2 ) và f ( x ) ≠ 0 , ∀ x ∈ R . Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=2 là

A. y=-2x+4.

B. y=2x+4.

C. y=2x.

D. y=4x+4.

Cho hàm số y = f(x) có đạo hàm f'(x)>0, ∀ x ∈ 1 ; 2 thỏa mãn f(1) = 1, f(2) = 22/14 và ∫ 1 2 f ' x 3 x 4 d x = 7 375 . Tích phân ∫ 1 2 f x d x  bằng

A. .

B. .

C. .

D. .

Cho hàm số y=f(x) thỏa mãn f ' ( x ) + 2 x f ( x ) = e - x 2 ,   ∀ x ∈ R  và f(1)=0 Tính giá trị f(2).

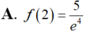
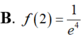
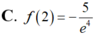
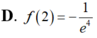
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1   là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là

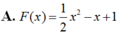
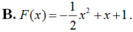
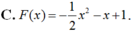
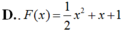
Cho hàm số y=f(x) xác định và liên tục trên [0;2] thỏa mãn  e x f 2 ( x ) + f ( x ) = f ' ( x ) - 1 e x  và f(0)=1. Tính f(2). 

A.  1 e 2

B.  - 5 3 e 2

C.  - 1 e 2

D.  - 2 3 e 2