Cho hình nón có bán kính đáy r = 1 chiều cao h = 3 Tính diện tích xung quanh S x q của hình nón đó.
A. S x q = 2 3 π .
B. S x q = 3 π .
C. S x q = 4 π .
D. S x q = 2 π .
Những câu hỏi liên quan
Cho hình nón có bán kính đáy r 1, chiều cao h
3
. Tính diện tích xung quanh
S
x
q
của hình nón đó.
Đọc tiếp
Cho hình nón có bán kính đáy r = 1, chiều cao h = 3 . Tính diện tích xung quanh S x q của hình nón đó.
Cho hình nón có bán kính đáy r1, chiều cao
h
3
Tính diện tích xung quanh
S
x
q
của hình nón đó A.
S
x
q
2
3
π
B.
S
x
q
3
π
C. ...
Đọc tiếp
Cho hình nón có bán kính đáy r=1, chiều cao h = 3 Tính diện tích xung quanh S x q của hình nón đó
A. S x q = 2 3 π
B. S x q = 3 π
C. S x q = 4 π
D. S x q = 2 π
Cho hình nón có bán kính đáy R 3(cm) và chiều cao h 4(cm). Diện tích xung quanh của hình nón là: A. 25
π
(
c
m
2
) B. 12
π
(
c
m
2
) C. 20
π
(
c
m
2
) D. 15
π
(
c
m
2
)
Đọc tiếp
Cho hình nón có bán kính đáy R = 3(cm) và chiều cao h = 4(cm). Diện tích xung quanh của hình nón là:
A. 25 π ( c m 2 )
B. 12 π ( c m 2 )
C. 20 π ( c m 2 )
D. 15 π ( c m 2 )
Cho hình nón có bán kính đáy R 3(cm) và chiều cao h 4(cm). Diện tích xung quanh của hình nón là: A. 25
π
(
c
m
2
) B. 12
π
(
c
m
2
) C. 20
π
(
c
m
2
) D. 15
π
(
c
m
2
)
Đọc tiếp
Cho hình nón có bán kính đáy R = 3(cm) và chiều cao h = 4(cm). Diện tích xung quanh của hình nón là:
A. 25 π ( c m 2 )
B. 12 π ( c m 2 )
C. 20 π ( c m 2 )
D. 15 π ( c m 2 )
Cho hình nón (N) có chiều cao h = 4, bán kính đường tròn đáy r = 3. Diện tích xung quanh của hình nón (N) bằng:
A. 12 π
B. 20 π
C. 15 π
D. 30 π
Chọn C.
Ta có S xq = πrl = πr h 2 + r 2 = 15 π .
Đúng 0
Bình luận (0)
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
Đọc tiếp
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
Hình nón tròn xoay có chiều cao h=3a bán kính đường tròn đáy r=3 Thể tích khối nón bằng
Cho hình nón có bán kính đáy
R
a
và chiều cao
h
a
3
. Diện tích xung quanh của hình nón đã cho là
Đọc tiếp
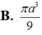
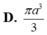
Cho hình nón có bán kính đáy R = a và chiều cao h = a 3 . Diện tích xung quanh của hình nón đã cho là
Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h. Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H). Xác định r để (H') có thể tích lớn nhất.
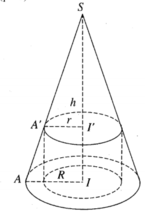
V H ' lớn nhất khi f(r) = r 2 (R - r) (với 0 < r < R) là lớn nhất. Khảo sát hàm số f(r), với 0 < r < R. Ta có f'(r) = 2Rr - 3 r 2 = 0, khi r = 0 (loại), hoặc r = 2R/3. Lập bảng biến thiên ta thấy f(r) đạt cực đại tại r = 2R/3.
Khi đó 
Đúng 0
Bình luận (0)