Cho log2 a =x và log2 b =y với a>0 b>0, b3# a3. Tìm biểu diễn của log a - 2 b 3 a 4 b theo x và y
![]()
![]()
![]()
![]()
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho tích phân ∫ - π 3 0 cos 2 x . cos 4 x d x = a + b 3 , trong đó a,b là các hằng số hữu tỷ. Tính e a + log 2 | b |
A. -2
B. -3
C. 1/8
D. 0
Biết rằng log 2 ( log 3 ( log 4 x ) ) = log 3 ( log 4 ( log 2 y ) ) = log 4 ( log 2 ( log 3 z ) ) = 0 . Tính tổng x + y + z
A. 50
B. 58
C. 89
D. 111
Chọn C
Ta có:
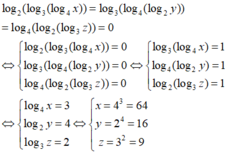
Từ đó x + y + z = 64 + 16 + 9 = 89
Xét các mệnh đề sau
(1) log2(x - 1)2 + 2log2(x+1) = 6
<=> 2log2(x-1) + 2log2(x+1) = 6
(2) log2(x2+1) ≥ 1 + log2|x|; ∀ x ∈ R
(3) xlny = ylnx; ∀ x > y > 2
( 4 ) log 2 2 2 x - 4 log 2 x - 4 = 0 ⇔ log 2 2 x - 4 log 2 x - 3 = 0
Số mệnh đề đúng là
A. 0
B. 1
C. 2
D. 3
Đáp án C
Dựa vào giả thiết, ta thấy rằng:
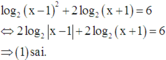
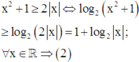
đúng.
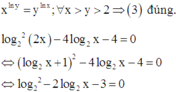
=> (4) sai. Vậy có 2 mệnh đề đúng.
Nghiệm của bất phương trình log 2 ( 3 x - 2 ) < 0 là:
A. x > 1 B. x < 1
C. 0 < x < 1 D. log 3 2 < x < 1
Tổng các nghiệm của phương trình log 2 ( x - 2 ) + log 2 ( x - 4 ) 2 = 0 bằng
A. 9
B. 3 + 2
C. 12
D. 6 + 2
Biết rằng phương trình 3 log 2 2 x - log 2 x - 1 = 0 có hai nghiệm là a, b. Khẳng định nào sau đây là đúng?
A. a + b = 1 3
B. a b = - 1 3
C. a b = 2 3
D. a + b = 2 3
Đáp án C
Phương trình
3 log 2 2 x - log 2 x - 1 = 0
→ log 2 a + log 2 b = 1 3 ⇔ log 2 a b = 1 3 ⇔ a b = 2 3
Nghiệm của phương trình log 4 { 2 log 3 [ 1 + log 2 ( 1 + 3 log 2 x ) ] } = 1/2 là
A. x = 1 B. x = 2
C. x = 3 D. x = 0
Cho a,b là các số nguyên dương thỏa mãn: log2(log2a(log2b21000)) = 0. Tính giá trị lớn nhất của ab
\(\Rightarrow log_{2^a}\left(log_{2^b}2^{1000}\right)=1\)
\(\Rightarrow log_{2^b}2^{1000}=2^a\)
\(\Rightarrow\dfrac{1000}{b}=2^a\)
\(\Rightarrow\dfrac{1000}{2^a}=b\)
\(\Rightarrow\dfrac{2^3.125}{2^a}=b\)
Do a;b nguyên dương \(\Rightarrow2^3⋮2^a\Rightarrow a=\left\{1;2;3\right\}\)
Giờ thì tìm b tương ứng a rồi tính 3 giá trị a.b, so sánh => đáp án