Ta có: (d1): y=mx-y=2

\(\Leftrightarrow y=mx-2\)

\(\Leftrightarrow y+2=mx\)

Tọa độ điểm B cố định là nghiệm của hệ phương trình:

\(\left\{{}\begin{matrix}y+2=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\x=0\end{matrix}\right.\)

Vậy: (d1) luôn đi qua B(0;-2)

Ta có: (d2): (2-m)x+y=m

\(\Leftrightarrow y=mx-2x+m\)

\(\Leftrightarrow y+2x=m\left(x+1\right)\)

Tọa độ điểm C cố định là nghiệm của hệ phương trình:

\(\left\{{}\begin{matrix}x+1=0\\y+2x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2x=-2\cdot\left(-1\right)=2\end{matrix}\right.\)

Vậy: (d2) luôn đi qua điểm C(-1;2)

Gọi \(B\left(x_B;y_B\right)\) là điểm cố định mà \(\left(d_1\right)\) đi qua

\(\Rightarrow mx_B-y_B=2\Rightarrow mx_B-\left(y_B+2\right)=0\Rightarrow\left\{{}\begin{matrix}x_B=0\\y_B=-2\end{matrix}\right.\)

\(\Rightarrow B\left(0;-2\right)\Rightarrow\left(d_1\right)\) luôn đi qua điểm \(B\left(0;-2\right)\) cố định 

Gọi \(C\left(x_C;y_C\right)\) là điểm cố định mà \(\left(d_2\right)\) đi qua

\(\Rightarrow\left(2-m\right)x_C+y_C=m\Rightarrow2x_C-mx_C-m+y_C=0\)

\(\Rightarrow-m\left(x_C+1\right)+2x_C+y_C=0\Rightarrow\left\{{}\begin{matrix}x_C=-1\\2x_C+y_X=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_C=-1\\y_C=2\end{matrix}\right.\)

\(\Rightarrow C\left(-1;2\right)\Rightarrow\left(d_2\right)\) luôn đi qua điểm \(C\left(-1;2\right)\) cố định

Đề thiếu m ở 3 hoặc -2 rồi ạ. 

\(y=mx^3+2mx^2+\left(1-m\right)x+3-2m\)

\(\Leftrightarrow\left(x^3+2x^2-x-2\right)m+\left(x-y+3\right)=0\)

Gọi \(\left(x_0\text{;}y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua. 

\(\Leftrightarrow\left\{{}\begin{matrix}x_0^3+2x_0^2-x_0-2=0\left(a\right)\\x_0-y_0+3=0\end{matrix}\right.\)

PT (a) có 3 nghiệm phân biệt nên đồ thị hàm số luôn đi qua 3 điểm cố định. 

Giải pt ra 3 điểm đó là \(A\left(1\text{;}4\right),B\left(-1\text{;}2\right),C\left(-2\text{;}1\right)\)

\(\overrightarrow{AB}=\left(-2\text{;}-2\right)\)

\(\overrightarrow{AC}=\left(-3\text{;}-3\right)\)

\(\overrightarrow{AB}=\dfrac{2}{3}\overrightarrow{AC}\) => Vector AB và vector AC cùng hướng. 

Vậy 3 điểm A, B, C thẳng hàng. 

???

what?

e đồng ý gì thế =)

Gọi 2 điểm cố định là \(A\left(x_0;y_0\right)\)

Thay vào ptđt (d) ta được : \(y_0=mx_0+m+1\Leftrightarrow mx_0+m+1-y_0=0\)

\(\Leftrightarrow m\left(x_0+1\right)+\left(1-y_0\right)=0\)

Đẳng thức xảy ra khi \(\hept{\begin{cases}x_0+1=0\\1-y_0=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=1\end{cases}}\Rightarrow A\left(-1;1\right)\)

Vậy d luôn đi qua 1 điểm cố định A(-1;1) 

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình :

14.x2=x−114.x2=x−1

<=> x² = 4x - 4

<=> x² - 4x + 4 = 0 <=> (x - 2)² = 0 <=> x - 2= 0 <=> x = 2

=> y = 2-1 = 1

Vậy (P) cắt (d) tại 1 điểm duy nhất là (2;1) 

=> đpcm 

đúng ko ????????????? 

sai thì cho mik xin lỗi

a/ Gọi điểm cố định \(M\left(x_0;y_0\right)\)

Khi đó đường thẳng y = k(x+3)-7 đi qua M , tức \(k\left(x_0+3\right)-7-y_0=0\) 

Vì đường thẳng y = k(x+3)-7 luôn đi qua M nên \(\hept{\begin{cases}x_0+3=0\\-y_0-7=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=-3\\y_0=-7\end{cases}}\)

Vậy đường thẳng đã cho luôn đi qua điểm M(-3;-7)

b/ Gọi điểm cố định là \(N\left(x_0;y_0\right)\)

Vì họ đường thẳng (m+2)x + (m-3)y -m+8 = 0 luôn đi qua N nên : 

\(\left(m+2\right).x_0+\left(m-3\right).y_0-m+8=0\)

\(\Leftrightarrow m\left(x_0+y_0-1\right)+\left(2x_0-3y_0+8\right)=0\)

Ta có \(\hept{\begin{cases}x_0+y_0-1=0\\2x_0-3y_0+8=0\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=2\end{cases}}\)

Vậy điểm cố định N(-1;2)

Câu còn lại bạn làm tương tự nhé ^^

c/ Đơn giản thôi mà =)

Ta cũng gọi điểm cố định đó là \(M\left(x_0;y_0\right)\)

Vì họ đường thẳng y=(2-k)x+k-5 đi qua M nên : 

\(y_0=\left(2-k\right)x_0+k-5\Leftrightarrow k\left(1-x_0\right)+\left(2x_0-y_0-5\right)=0\)

Ta có \(\hept{\begin{cases}1-x_0=0\\2x_0-y_0-5=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=1\\y_0=-3\end{cases}}\)

Vậy điểm cố định là M(1;-3)

Giả sử ( x 0 ; y 0  ) là điểm cố định mà đường thẳng mx + 3 + (3m – 1)y = 0 luôn đi qua.

Ta có:

m x 0  + 3 + (3m - 1)  y 0  = 0 với mọi m

⇔ m x 0  + 3 + 3m y 0  - y 0  = 0 với mọi m

⇔ m( x 0  + 3 y 0 ) + 3 - y 0 = 0 với mọi m

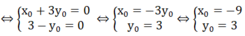
Vậy điểm cố định mà đường thẳng luôn đi qua là (-9: 3)