Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, B C = 2 a , A B C ⏞ = 60 ° . Gọi M là trung điểm của BC Biết SA=SB=SM= a 39 3 Khoảng cách từ S đến mặt phẳng (ABC)
A. 2a
B. 4a
C. 3a
D. a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. ; AB = a, AC= a 3 .Tam giác SAB, SAC lần lượt vuông tại B và C. Khối cầu ngoại tiếp hình chóp S.ABC có thể tích bằng 5 5 6 πa 3 . Tính thể tích khối chóp S.ABC
A. a 3 3 3
B. a 3 3 2
C. a 3 3 12
D. a 3 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=a, AC=2a. Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 2 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
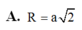
![]()
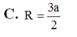
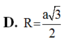
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a, AC = 2a. Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 3 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
A. R = a 2
B. R = a
C. R = 3 a 2
D. R = a 3 2
Hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=a, AC=2a. Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 3 Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
![]()
![]()
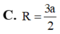
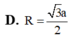
Hình chóp S . A B C có đáy ABC là tam giác vuông tại A , A B = a , A C = 2 a . Mặt bên S A B , S C A lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 3 . Bán kính mặt cầu ngoại tiếp hình chóp S . A B C là
A. R = a 2
B. R = a
C. R = 3 a 2
D. R = 3 a 2
Đáp án C

Kẻ hinh chữ nhật A B C D như hình vẽ bên ⇒ S D ⊥ A B C D
Diện tích tam giác ABC là S A B C = 1 2 . A B . A C = a 2
Suy ra V S . A B C = 1 3 . S D . S Δ A B C = a 2 3 . S D = 2 3 a 3 ⇒ S D = 2 a .
Bán kính mặt cầu ngoại tiếp khối chóp S . A B D C là
R = R A B D C 2 + S D 2 4 = a 5 2 2 + 2 a 2 4 = 3 a 2
Vậy bán kính mặt cầu cần tính là R = 3 a 2 .
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại B, AB=a, ∠ A B C = 45 ° cạnh bên SA vuông góc với mặt phẳng đáy một góc 60 ° . Tính thể tích V của khối chóp S.ABC
A. V = a 3 3 9
B. V = a 3 3 6
C. V = a 3 4 3
D. V = a 3 3 18
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A; A B = 1 c m ; A C = 3 c m . Tam giác SAB, SAC lần lượt vuông tại B và C. Khối cầu ngoại tiếp hình chóp S.ABC có thể tích bằng 5 5 π 6 c m 3 . Tính khoảng cách từ C tới (SAB) .
A. 3 2 c m
B. 5 2 c m
C. 3 4 c m
D. 5 4 c m
Gọi I là trung điểm của SA.
Tam giác SAB, SAC vuông tại B , C ⇒ I S = I A = I B = I C ⇒ I là tâm mặt cầu ngoại tiếp chóp S.ABC.
Gọi H là trung điểm của BC. Vì vuông tại là tâm đường tròn ngoại tiếp tam giác ABC.
⇒ I H ⊥ A B C .
Gọi R là bán kính mặt cầu ngoại tiếp chóp S.ABC. Theo bài ra ta có:

Xét tam giác vuông ABC có:
B C = A B 2 + A C 2 = 2 ⇒ A H = 1
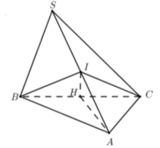
Xét tam giác vuông IAH có:
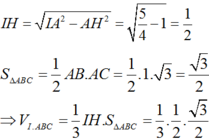
Ta có:
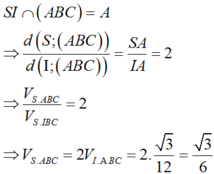
Xét tam giác vuông SAB có
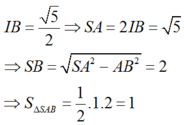
Ta có
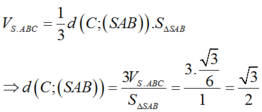
Chọn A.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh SA vuông (ABC) A) C/m: (SAB) vuông (ABC) B) C/m:(SAC)vuông (ABC) C) C/m:(SBC) vuông (SAB)
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại B, AB = a, A C B ^ = 45 o , cạnh bên SA vuông góc với mặt phẳng đáy một góc 60 o Tính thể tích V của khối chóp S.ABC
A. V = a 3 3 9
B. V = a 3 3 6
C. V = a 3 4 3
D. V = a 3 3 18
Đáp án B
Tam giác SAB vuông tại A có S B A ^ = 60 o nên SA= a 3
Tam giác ABC vuông cân tại B nên
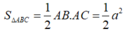
Do đó
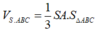
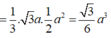
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = a cạnh bên SA vuông góc với đáy và SA = a. Tính diện tích toàn phần S t p của hình chóp S.ABC.
A. S t p = 2 a 2
B. S t p = a 2 1 + 2
C. S t p = a 2 1 + 2 2
D. S t p = 2 a 2 2