Cho số phức z thỏa mãn (3 + i).z - i.z =7 - 6i Mô đun của số phức z bằng:
A. 25
B. 2 5
C. 5
D. 5
Cho số phức z thỏa mãn ( 1+ i) z + 2z = 2. Tính mô-đun của số phức w = z + 2/5 - 4/5i.
A. 1.
B. 2.
C. 2
D. 3
Chọn C.
Đặt z = a+ bi.
Theo đề ra ta có: ( 3 + i) z = 2
Hay ( 3 + i)( a + bi) = 2
Suy ra: 3a - b + ( 3b + a) i = 2
![]()
nên z = 3/5 - 1/5i.
Khi đó w = 3/5 - 1/5i + 2/5 - 4/5 i = 1 - i.
Vậy ![]()
Cho số phức z thỏa mãn ( 3 + i ) z - i z = 7 - 6 i . Môđun của số phức z bằng
![]()
![]()
![]()
![]()
Tính mô-đun của số phức z thỏa mãn 1 + i z + 3 − i z ¯ = 2 − 6 i
A. z = 13
B. z = 15
C. z = 5
D. z = 3
Tính mô-đun của số phức z thỏa mãn 1 + i z + 3 - i z = 2 - 6 i
A. z = 13
B. z = 15
C. z = 5
D. z = 3
Đáp án A
Gọi z = x + y i , x , y ∈ ℤ → z = x - y i .
Từ giả thiết ta có 1 + i x + y i + 3 - i x - y i = 2 - 6 i
⇔ x - y + x + y i + 3 x - y - x + 3 y i = 2 - 6 i ⇔ 4 x - 2 y - 2 y i = 2 - 6 i
⇔ 4 x - 2 y = 2 - 2 y = - 6 ⇔ x = 2 y = 3 → z = 2 + 3 i → z = 2 2 + 3 2 = 13 .
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Tính mô đun của số phức z + i.
A. z + i = 61
B. z + i = 5 2
C. z + i = 3 5
D. z + i = 2 41
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z
A. | z | = 34
B. | z | = 34
C. | z | = 34 3
D. | z | = 5 34 3
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z.
A. z = 34
B. z = 34
C. z = 34 3
D. z = 5 34 3
Đáp án B
Phương pháp
Từ giả thiết ta biến đổi để tìm được công thức của z. Dùng định nghĩa để tìm z
Lời giải chi tiết.
Ta có:
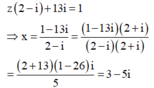
Do đó ![]()
Cho số phức z thỏa mãn z(2-i) + 13i = 1. Tính mô đun của số phức z.
A. |z| = 34
B. |z| = 34
C. |z| = 5 34 3
D. |z| = 34 3
Cho số phức z thỏa mãn z(2-i) + 13i = 1. Tính mô đun của số phức z.
A. |z| = 34
B. |z| = 34
C. |z| = 5 34 3
D. |z| = 34 3