Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y = -x + m cắt đồ thị hàm số y = x - 2 x - 1 tại hai điểm phân biệt A, B sao cho OA + OB = 4 (O là gốc tọa độ)?
A. 2
B. 1
C. 0
D. 3
Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y=m(x-4) cắt đồ thị của hàm số y = x 2 − 1 x 2 − 9 tại bốn điểm phân biệt?
A. 1
B. 5
C. 3
D. 7
Cho hàm số y = x 3 − 3 x 2 + 4 có đồ thị (C) như hình vẽ bên và đường thẳng d : y = m 3 − 3 m 2 + 4 (với m là tham số). Hỏi có bao nhiêu giá trị nguyên của tham số m để đường thẳng d cắt đồ thị (C) tại ba điểm phân biệt

A. 3
B. 1
C. 2
D. Vô số
Cho hàm số y = x + 2 x có đồ thị là (C) và đường thẳng d : y = x + m . Có tất cả bao nhiêu giá trị nguyên của tham số m trên đoạn 0 ; 2018 để đường thẳng (d) cắt (C) tại hai điểm phân biệt A;B sao cho tam giác MAB cân tại M, với M 1 2 ; 1 2 .
A. 2016
B. 2017
C. 2019
D. 2018
Đáp án D
Phương trình hoành độ giao điểm của )C) và(d) là
x + 2 x = x + m ⇔ x ≠ 0 x 2 + m − 1 x − 2 = 0 *
Để (C) cắt (d) tại 2 điểm phân biệt ⇔ * có 2 nghiệm phân biệt khác 0 ⇔ m ∈ ℝ
Khi đó, gọi A x 1 ; x 1 + 1 ; B x 2 ; x 2 + m ⇒ x 1 + x 2 = 1 − m là tọa độ giao điểm của (C) và(d)
Ta có: A B → = x 2 − x 1 ; x 2 − x 1 ⇒ u A B → = 1 ; 1 ; trung điểm AB là: I 1 − m 2 ; 1 + m 2
m = 0 ⇒ M , A , B thẳng hang (loại m = 0 )
Phương trình trung trực là: x + y − 1 = 0
Do M ∈ d ⇒ Δ M A D luôn cân tại M
Kết hợp với m ∈ ℤ và có 2018 giá trị m cần tìm
Cho hàm số y = 2 x + 3 x + 2 có đồ thị (C) và đường thẳng d: y = x + m Các giá trị của tham số m để đường thẳng (C) cắt đồ thị tại hai điểm phân biệt là:
A. m > 2
B. m > 6
C. m = 2
D. m < 2 hoặc m > 6
Cho hàm số y= x4- (2m-1) x2+2m có đồ thị (C) . Có tất cả bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y= 2 cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là
A. 1
B. 2
C. 3
D. 4
+ Phương trình hoành độ giao điểm của (C) và đường thẳng d:
=x4- (2m-1) x2+2m = 2 hay x4- (2m-1) x2+2m -2=0
Suy ra x2= 1 hoặc x2= 2m-2 (1)
+ Đường thẳng d cắt C tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương trình (1) có hai nghiệm phân biệt nhỏ hơn 3.
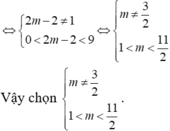
Do đó có 4 giá trị nguyên của m thỏa mãn đầu bài.
Chọn D.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 - m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt
A. 3
B. 2
C. 4
D. 1
Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
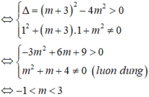
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
![]()
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt?
A. 3
B.. 4
C. 1
D. 2
Đáp án là A
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành:
![]()
![]()
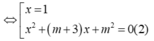
Đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ (2) có 2 nghiệm phân biệt khác 1
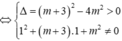
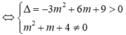
![]()
Do đó có 3 giá trị nguyên của m thỏa mãn ycbt.
Cho hàm số: y=x-3-3(m+1)x2+9x+m-2 (1) có đồ thị là (Cm). Có bao nhiêu giá trị nguyên của tham số m để (Cm) có điểm cực đại, cực tiểu đối xứng với nhau qua đường thẳng y=1/2x ?
A. 0
B. 1
C. 2
D. 3
Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 100 ) + m 2 có 5 điểm cực trị?

A. 0.
B. 1.
C. 2.
D. 4.