Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x + 2 y - z - 1 = 0 , (Q): 3x-(m+2)y+(2m-1)z+3=0. Tìm m để hai mặt phẳng (P), (Q)  vuông góc với nhau.

Trong không gian Oxyz, cho hai đường thẳng △ :   x - 1 - 2 = y + 2 1 = z - 3 2  và mặt phẳng (P): x+y-2z+6=0. Góc giữa đường thẳng △  với mặt phẳng (P) bằng

A. 30 °

B. 45 °

C. 60 °

D. 135 °

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x-y+z-1=0 và (Q):2x+y+1=0. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng (P) và (Q).

Trong không gian Oxyz, cho hai mặt phẳng (P):2x - y + z = 0, (Q):x - z = 0. Giao tuyến của hai mặt phẳng (P) và (Q) có một vectơ chỉ phương là:

A.  a ⇀ = (1; 0: -1)

B.  a ⇀  = (1; -3: 1)

C.  a ⇀  = (1; 3: 1)

D.  a ⇀  = (2; -1: 1)

Trong không gian Oxyz, cho ba mặt phẳng (P), (Q), (R) lần lượt có phương trình là ( m 2 + m)x - (m + 2)y + z = 0; x + y + z = 0; 2x + y - z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R)?

A. m = 1

B. m = -1

C. m = -3/2

D. m = -3/2 hoặc m = -1

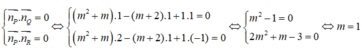
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng α :   x + y - z + 1 = 0   v à   β :   - 2 x + m y + 2 z - 2 = 0 . Tìm m để mặt phẳng (α) song song với mặt phẳng (β).

A. m = 2

B. m = 5

C. Không tồn tại

D. m = -2

Trong không gian Oxyz, cho hai mặt phẳng P :   2 x - 2 y + z - 2 = 0 và Q :   2 x - y + z + 1 = 0 . Số mặt cầu đi qua A(1;-2;1) và tiếp xúc với hai mặt phẳng (P), (Q) là

A. 1

B. 2

C. 0

D. Vô số