Cho đồ thị hàm bậc ba y=f(x) như hình vẽ. Hỏi hàm số y = x 2 + 4 x + 3 x 2 + x x f 2 ( x ) - 2 f ( x ) có bao nhiêu đường tiệm cận đứng.
A. 6.
B. 3.
C. 2.
D. 4.
Những câu hỏi liên quan
Cho hàm số bậc ba
y
f
x
, hàm số
y
f
x
có đồ thị như hình vẽ. Hỏi hàm số
g
x
f
−
x
−
x
2
nghịch biến trên khoảng nào dưới đây? A. (-2;-1) B. (1;2) C. (-1;0) D.
−...
Đọc tiếp
Cho hàm số bậc ba y = f x , hàm số y = f ' x có đồ thị như hình vẽ. Hỏi hàm số g x = f − x − x 2 nghịch biến trên khoảng nào dưới đây?
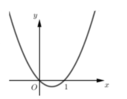
A. (-2;-1)
B. (1;2)
C. (-1;0)
D. − 1 2 ; 0
Cho hàm số bậc ba
y
f
(
x
)
có đồ thị như hình vẽ bên. Tìm tham số m để hàm số
y
f
(
x
)
+
m
có ba điểm cực trị?
Đọc tiếp
Cho hàm số bậc ba y = f ( x ) có đồ thị như hình vẽ bên. Tìm tham số m để hàm số y = f ( x ) + m có ba điểm cực trị?
Cho hàm số bậc ba
y
f
x
có đồ thị như hình vẽ. Hỏi đồ thị hàm số
y
x
+
1
x
+
3
x
x
+
1...
Đọc tiếp
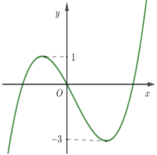
Cho hàm số bậc ba y = f x có đồ thị như hình vẽ.
Hỏi đồ thị hàm số y = x + 1 x + 3 x x + 1 x - 1 f x f x - 2 có bao nhiêu tiệm cận đứng
A. 1
B. 2
C. 4
D. 5
Cho hàm số bậc ba f(x)
x
3
+
b
x
2
+
c
x
+
d
. Biết đồ thị của hàm số y f(x) như hình vẽ. Giá trị của
c
b
là A. -
1
3
B.
3
4
C.
1
3
D. -
3
4
Đọc tiếp
Cho hàm số bậc ba f(x) = x 3 + b x 2 + c x + d . Biết đồ thị của hàm số y = f'(x) như hình vẽ. Giá trị của c b là
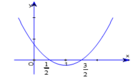
A. - 1 3
B. 3 4
C. 1 3
D. - 3 4
Chọn D
Tập xác định D = ℝ
Đạo hàm cấp 1 
Dựa vào đồ thị của hàm số y = f'(x) ta có bảng thiên của hàm số f(x)
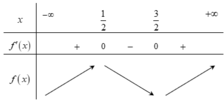
Ta có 
Dựa vào bảng biến thiên ta có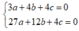 
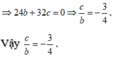
Đúng 0
Bình luận (0)
Biết rằng đồ thị hàm số bậc 4: y f(x) được cho như hình vẽ sau:Tìm số giao điểm của đồ thị hàm số y g(x) [f’(x)]2 – f(x).f’’(x) và trục Ox A. 0 B. 2 C. 4 D. 6
Đọc tiếp
Biết rằng đồ thị hàm số bậc 4: y = f(x) được cho như hình vẽ sau:
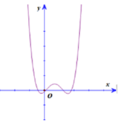
Tìm số giao điểm của đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) và trục Ox
A. 0
B. 2
C. 4
D. 6
Đáp án A
Phương pháp:
Đặt Đáp án A
Phương pháp:
Đặt f(x) = a(x – x1)(x – x2)(x – x3)(x – x4), tính đạo hàm của hàm số y = f(x)
Xét hàm số h x = f ' x f x và chứng minh f(x).f’’(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Cách giải: Đồ thị hàm sốy = f(x) cắt trục hoành tại bốn điểm phân biệt nên
f(x) = a(x – x1)(x – x2)(x – x3)(x – x4)
=> f ’(x) = a(x – x1)(x – x2)(x – x3)(x – x4) + a(x – x1)(x – x3)(x – x4) + a(x – x1)(x – x2)(x – x4) + a(x – x1)(x – x2)(x – x3)
f ’(x) = f(x) 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4 => f’(x) ≠ 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Đặt h x = f ' x f x = 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Ta có
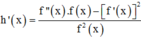
= - 1 ( x - x 1 ) 2 + - 1 ( x - x 2 ) 2 + - 1 ( x - x 3 ) 2 + - 1 ( x - x 4 ) 2 <0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> f ''(x).f(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> g(x) = [f’(x)]2 – f(x).f’’(x)>0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Khi f(x) = 0 => f '(x) ≠ 0 => g(x) = [f’(x)]2 – f(x).f’’(x) ≠ 0
Vậy đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) không cắt trục Ox
Đúng 0
Bình luận (0)
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình f(x)=3
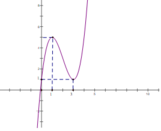
A. 0
B. 2
C. 1
D. 3
Cho hàm số bậc ba y f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số
y
f
(
x
)
+
m
có 3 điểm cực trị? A. 1 ≤ m ≤ 3 B. m -1 hoặc m 3 C. m ≤ -1 hoặc m ≥ 3 D. m ≤ -3 hoặc m ≥ 1
Đọc tiếp
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x ) + m có 3 điểm cực trị?
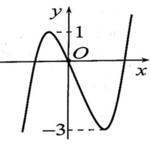
A. 1 ≤ m ≤ 3
B. m = -1 hoặc m = 3
C. m ≤ -1 hoặc m ≥ 3
D. m ≤ -3 hoặc m ≥ 1
Cho hàm số y f(x) và hàm số bậc ba y g(x) có đồ thị như hình vẽ bên. Diện tích phần gạch chéo được tính bởi công thức nào sau đây?
A
.
S
∫
-
3
-
1
[
f
(
x
)
-
g
(
x
)
]
dx
+
∫
-
1...
Đọc tiếp
Cho hàm số y = f(x) và hàm số bậc ba y = g(x) có đồ thị như hình vẽ bên. Diện tích phần gạch chéo được tính bởi công thức nào sau đây?
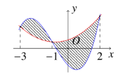
A . S = ∫ - 3 - 1 [ f ( x ) - g ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
B . S = | ∫ - 3 2 [ f ( x ) - g ( x ) ] dx |
C. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ f ( x ) - g ( x ) ] dx
D. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
Cho hàm số bậc ba yf(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số
y
f
(
x
-
1
)
-
m
-
1
có 3 điểm cực trị? A. -1m5 B.
-
1
≤
m
≤
5
C.
m...
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x - 1 ) - m - 1 có 3 điểm cực trị?
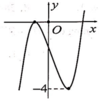
A. -1<m<5
B. - 1 ≤ m ≤ 5
C. m ≥ - 1 hoặc m ≤ - 5
D. m>-1 hoặc m<-5
