Giải pt lượng giác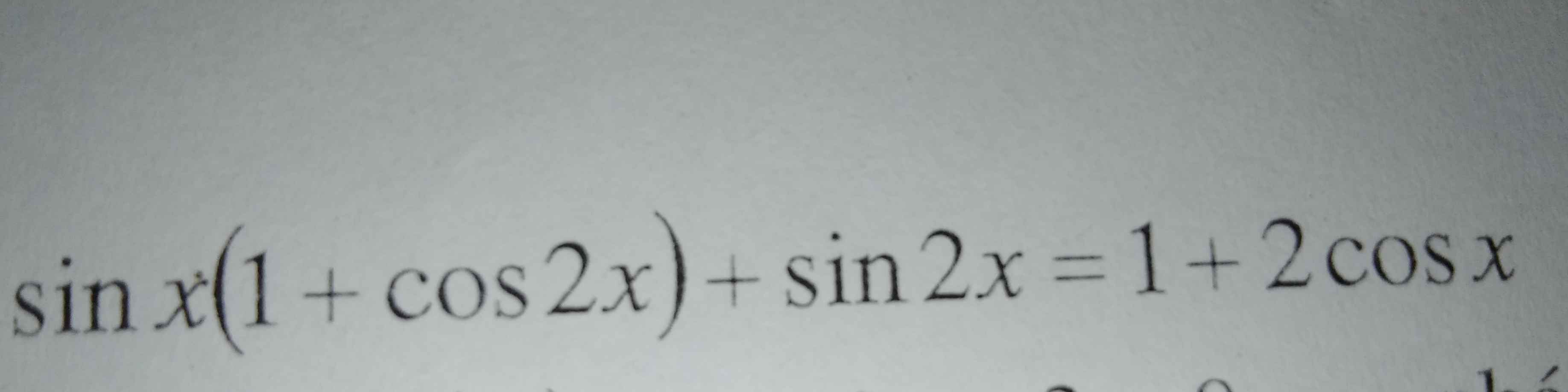

Những câu hỏi liên quan
Giải pt lượng giác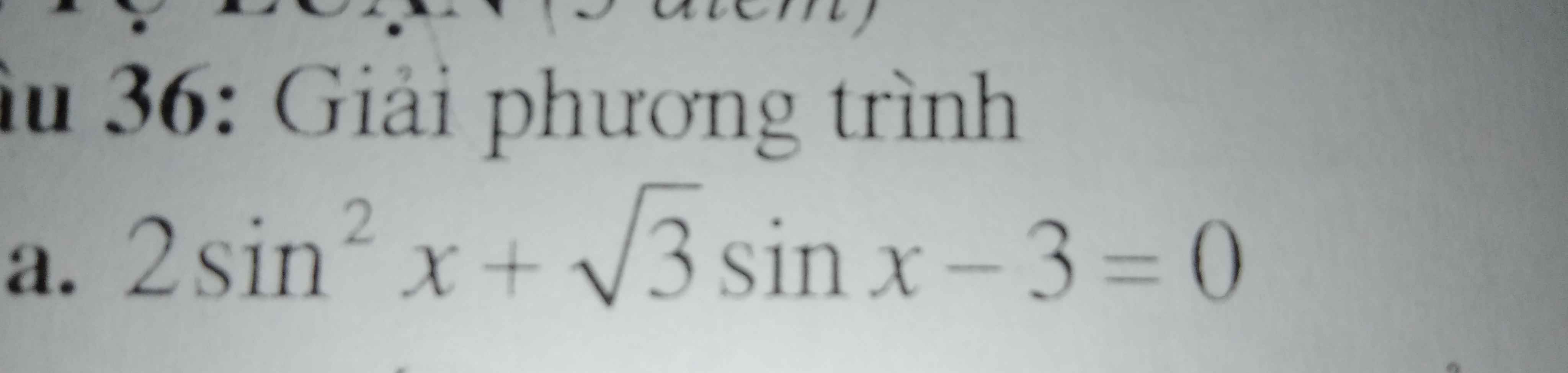
\(2sin^2x+\sqrt{3}sinx-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{\sqrt{3}}{2}\\sinx=-\sqrt{3}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Giải pt lượng giác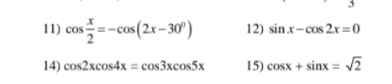
11.\(cos\dfrac{x}{2}=-cos\left(2x-30^0\right)\)
\(\Leftrightarrow cos\dfrac{x}{2}=-cos\left(2x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow cos\dfrac{x}{2}=cos\left(2x+\dfrac{5\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{x}{2}=2x+\dfrac{5\pi}{6}+k2\pi\\\dfrac{x}{2}=-2x-\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)(\(k\in Z\))\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5\pi}{9}-\dfrac{k4\pi}{3}\\x=-\dfrac{\pi}{3}+\dfrac{k4\pi}{5}\end{matrix}\right.\)(\(k\in Z\))
Vậy...
12) \(sinx-cos2x=0\Leftrightarrow sinx-1+2sin^2x=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}sinx=sin\dfrac{\pi}{6}\\sinx=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\x=\dfrac{-\pi}{2}+k2\pi\end{matrix}\right.\)(\(k\in Z\))
Vậy...
Đúng 2
Bình luận (2)
14)\(cos2x.cos4x=cos3x.cos5x\)
\(\Leftrightarrow\dfrac{1}{2}\left(cos2x+cos6x\right)=\dfrac{1}{2}\left(cos2x+cos8x\right)\)
\(\Leftrightarrow cos6x=cos8x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-k\pi\\x=\dfrac{k\pi}{7}\end{matrix}\right.\)(\(k\in Z\))
Vậy...
15. \(cosx+sinx=\sqrt{2}\)
\(\Leftrightarrow\dfrac{1}{\sqrt{2}}.cosx+\dfrac{1}{\sqrt{2}}.sinx=1\)
\(\Leftrightarrow sin\left(\dfrac{\pi}{4}+x\right)=1\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k2\pi\) (\(k\in Z\))
Vậy...
Đúng 1
Bình luận (0)
Giải pt lượng giác
13) \(sinxsin3x=\dfrac{1}{2}cos2x\)
\(\Leftrightarrow\dfrac{1}{2}\left(cos2x-cos4x\right)=\dfrac{1}{2}cos2x\)
\(\Leftrightarrow cos2x-cos4x=cos2x\)
\(\Leftrightarrow cos4x=0\)
\(\Leftrightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{8}\)( k∈Z)
b) \(\left(2sin\dfrac{x}{3}-1\right)tanx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2sin\dfrac{x}{3}-1=0\\tanx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\dfrac{x}{3}=\dfrac{1}{2}\\x=k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{x}{3}=\dfrac{\pi}{6}+k2\pi\\x=k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+\dfrac{k2\pi}{3}\\x=k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
Chúc bạn học tốt^^
Đúng 2
Bình luận (0)
Giải pt lượng giác
\(2sin\left(x+\dfrac{\pi}{6}\right)-\sqrt{3}=0\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)=sin\left(\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{6}=\pi-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\left(k\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\left(k\in Z\right)}\)
Đúng 0
Bình luận (3)
Giải pt lượng giác sau Cos3x=căn2/2
\(cosx=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+k2\pi\)
Đúng 0
Bình luận (0)
Giải pt lượng giác
Giúp em với em cảm ơn ạ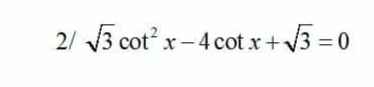
Giải pt lượng giác
Giúp em với em cảm ơn ạ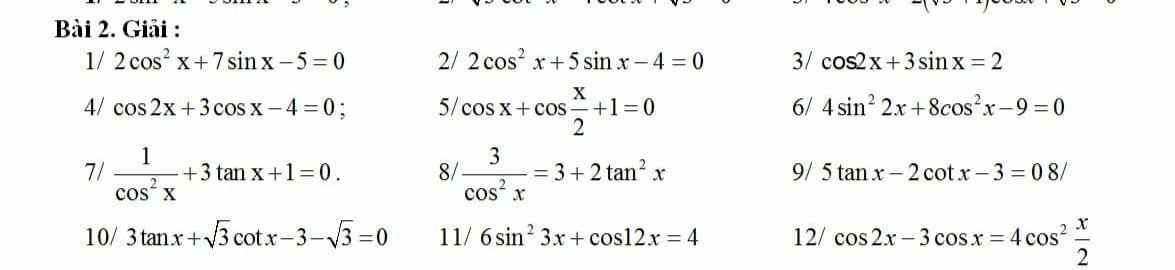
Giải pt lượng giác
Giúp em với em cảm ơn ạ
\(\Leftrightarrow\left(sinx-3\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=3>1\left(loại\right)\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải pt lượng giác
Giúp em với em cảm ơn ạ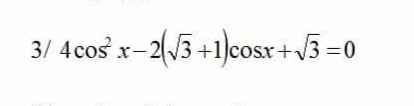
\(\Leftrightarrow\left(2cosx-1\right)\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Rightarrow x=...\)
Đúng 1
Bình luận (0)











