Câu 3: ( 3 điểm) Cho đoạn thẳng AB = 3 cm.
Nêu cách vẽ, ký hiệu đường trung trực của đoạn thẳng AB.
Chọn đoạn thẳng AB dài 24mm. Hãy vẽ đường trung trực của đoạn thẳng ấy. Nói rõ cách vẽ.
Đường trung trực của một đoạn thẳng AB là đường thẳng vuông góc với AB tại trung điểm của AB
- Vẽ đoạn thẳng AB = 24mm
- Vẽ trung điểm I cuả AB
Vì I là trung điểm của AB nên IA = IB = AB/2 = 12 (mm)
Đặt thước thẳng trùng với đường thẳng AB sao cho vạch 0 trùng với điểm A , vạch 12 cho ta vị trí điểm I.
- Vẽ đường thẳng d đi qua I và d⊥ AB
Đặt êke sao cho một cạnh góc vuông của êke trùng với đường thẳng AB, đỉnh góc vuông của êke trùng với I, vẽ đường thẳng đi qua cạnh góc vuông còn lại của êke ta được đường thẳng d.
Khi đó d là trung trực của AB.
a) Vẽ tam giác ABC. Vẽ các đường trung trực của các đoạn thẳng AB,BC,CA
b) Vẽ đường tròn tâm O bán kính R= 3(cm). Lấy 3 điểm A,B,C. Vẽ các đường trung trực của các đoạn thẳng AB,BC,CA
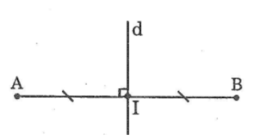
Vẽ hai đường thẳng aa' và bb' vuông góc với nhau tại M, trên đường thẳng aa' lấy hai điểm A, B sao cho M là trung điểm của AB. Trên đường thẳng bb' lấy hai điểm C, D sao cho CM=MD. Ghi đầy đủ kí hiệu lên hình vẽ và chứng tỏ đường thẳng bb' là đường trung trực của đoạn thẳng AB và đường thẳng aa' là đường trung trực của đoạn thẳng CD.
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
Vẽ đoạn thăng AB dài 3 cm. Vẽ đường trung trực của đoạn thẳng ấy. Nói rõ cách vẽ.
Chia đoạn thẳng thành 2 phần bằng nhau , Chấm một điểm I vào trung điểm của đoạn thẳng đó .
Đưa một cạnh của eke khớp với đoạn AI hoặc BI
Góc vuông của eke khớp vs điểm I(trung điểm)
Kẻ một đường thẳng qua I theo cạnh còn lại của eke .
- Vẽ đoạn thẳng AB = 3 cm
-Lấy M là trung điểm của đoạn thẳng AB
-Vẽ d đi qua đoạn thẳng AB và vuông góc tại M
=> d là đường trung trực của đoạn thẳng AB
a) Vẽ tam giác ABC. Vẽ các đường trung trực của các đoạn thẳng AB, BC, CA
b) Vẽ đường tròn tâm O bán kính R = 3(cm). Lấy 3 điểm A, B, C phân biệt bất kì trên đường tròn. Vẽ các dây AB, BC, CA. Vẽ các đường trung trực của đoạn thẳng AB, BC, CA
vẽ BAC=120 độ sao cho đoạn thẳng AB=2cm, AC=3cm. Vẽ đường trung trực d1 của đoạn thẳng AB, đường trung trực d2 của đoạn thẳng AC. 2 đường thẳng d1 và d2 cách nhau tại O. Viết 1 đề bài khác cho hình vẽ
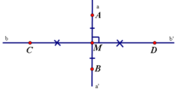
Bài 1: Cho đoạn thẳng AB = 4cm. Vẽ đường thẳng d là đường trung trực của đoạn thẳng AB. Lấy điểm O thuộc d. Qua O vẽ đoạn thẳng OC = 2cm sao cho OC vuông góc với d. Qua O vẽ đoạn thẳng OD = 1cm sao cho OD vuông góc với d.
a. Chứng tỏ 3 điểm C, O, D thẳng hàng.
b. Đường thẳng d có phải là trung trực của CD không? Vì sao?
Vì thẳng hàng
Vì , ⇒ không phải trung điểm của
Mà không phải đường trung trực của

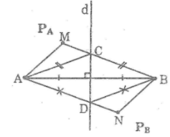
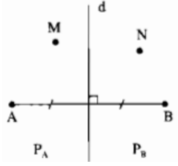
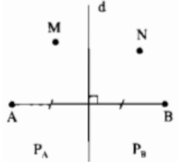
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên). Gọi N là một điểm của PB. Chứng minh rằng NB < NA
Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB.
Ta có: NA = ND + DA
mà DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ΔNDB, ta có:
NB < ND + DB (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên). Gọi M là một điểm của PA. Chứng minh rằng MA < MB
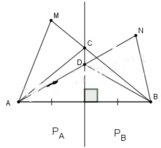
Nối MA, MB. Gọi C là giao điểm của MB với đường thẳng d, nối CA.
Ta có: MB = MC + CB
mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ΔMAC ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB