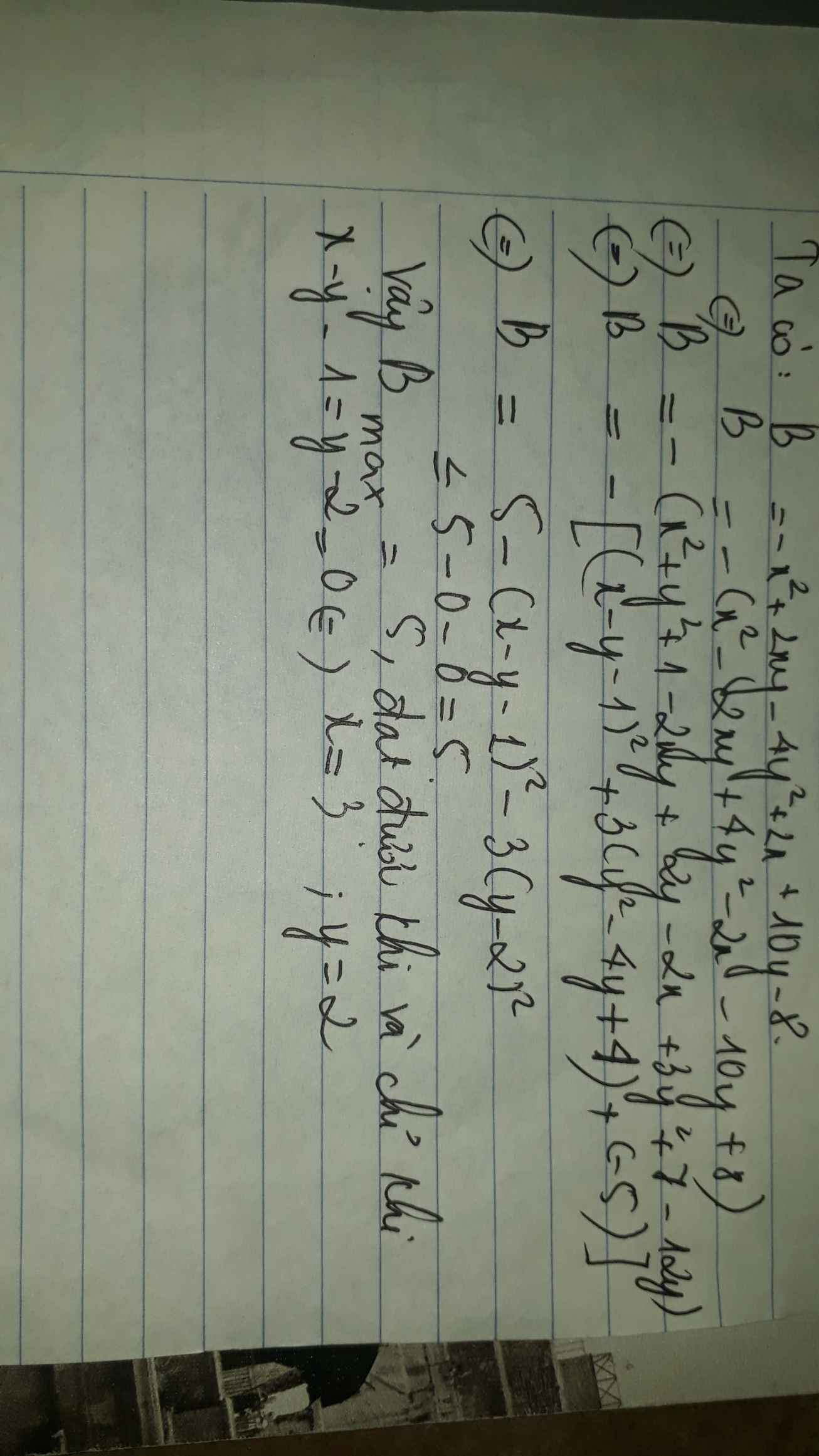\(Q=-2\left(x-\dfrac{3}{2}\right)^2+\dfrac{25}{2}\le\dfrac{25}{2}\)

\(Q_{max}=\dfrac{25}{2}\) khi \(x=\dfrac{3}{2}\)

\(A=\dfrac{9\left(x^2+2\right)-9x^2+6x-1}{x^2+2}=9-\dfrac{\left(3x-1\right)^2}{x^2+2}\le9\)

\(A_{max}=9\) khi \(x=\dfrac{1}{3}\)

\(A=\dfrac{12x+34}{2\left(x^2+2\right)}=\dfrac{-\left(x^2+2\right)+x^2+12x+36}{2\left(x^2+2\right)}=-\dfrac{1}{2}+\dfrac{\left(x+6\right)^2}{2\left(x^2+2\right)}\le-\dfrac{1}{2}\)

\(A_{min}=-\dfrac{1}{2}\) khi \(x=-6\)

`A=-x^2+2x+10`

`=-(x^2-2x)+10`

`=-(x-1)^2+11<=11`

Dấu "=" xảy ra khi `x=1`.

`B=4x-2x^2+8`

`=-2(x^2-2x)+8`

`=-2(x^2-2x+1)+10`

`=-2(x-1)^2+10<=10`

Dấu "=" xảy ra khi `x=1`

`C=-x^2-x+1`

`=-(x^2+x)+1`

`=-(x^2+x+1/4)+1+1/4`

`=-(x+1/2)^2+5/4<=5/4`

Dấu "=" xảy ra khi `x=-1/2`

`D=-4x^2+6x+3`

`=-(4x^2-6x)+3`

`=-(4x^2-6x+9/4)+21/4`

`=-(2x-3/2)^2+21/4<=21/4`

Dấu "=' xảy ra khi `2x=3/2<=>x=3/4`

\(a,A=-x^2+2x+10=-x^2+2x-1+11=-\left(x^2-2x+1\right)+11\)

\(=11-\left(x-1\right)^2\)

- Thấy : \(\left(x-1\right)^2\ge0\forall x\in R\)

\(\Rightarrow A=11-\left(x-1\right)^2\le11\)

Vậy MaxA = 11 <=> x = 1 .

\(b,B=-2x^2+4x-2+10=-2\left(x^2-2x+1\right)+10=10-2\left(x-1\right)^2\)

- Thấy : \(\left(x-1\right)^2\ge0\forall x\in R\)

\(\Rightarrow B=10-2\left(x-1\right)^2\le10\)

Vậy MaxB = 10 <=> x = 1 .

\(c,C=-x^2-\dfrac{1}{2}.2.x-\dfrac{1}{4}+\dfrac{5}{4}=\dfrac{5}{4}-\left(x+\dfrac{1}{2}\right)^2\)

- Thấy : \(\left(x+\dfrac{1}{2}\right)^2\ge0\forall x\in R\)

\(\Rightarrow C=\dfrac{5}{4}-\left(x+\dfrac{1}{2}\right)^2\le\dfrac{5}{4}\)

Vậy MaxC = 5/4 <=> x = -1/2 .

\(d,D=-4x^2+6x+3=-4x^2+2x.2.\dfrac{6}{4}-\dfrac{9}{4}+\dfrac{21}{4}=-\left(4x^2-6x+\dfrac{9}{4}\right)+\dfrac{21}{4}\)

\(=\dfrac{21}{4}-\left(2x-\dfrac{3}{2}\right)^2\)

- Thấy : \(\left(2x-\dfrac{3}{2}\right)^2\ge0\forall x\in R\)

\(\Rightarrow A=\dfrac{21}{4}-\left(2x-\dfrac{3}{2}\right)^2\le\dfrac{21}{4}\)

Vậy MaxD=21/4 <=> x = 3/4 .

\(\frac{x+2}{x^2+4}\in Z\Rightarrow x+2⋮x^2+4\)

\(\Rightarrow\left(x+2\right)\left(x-2\right)⋮x^2+4\)

\(\Rightarrow x^2-4⋮x^2+4\)

Mà \(x^2+4⋮x^2+4\)

\(\Rightarrow\left(x^2+4\right)-\left(x^2-4\right)⋮x^2+4\)

\(\Rightarrow8⋮x^2+4\)

\(\Rightarrow x^2+4\inƯ\left(8\right)\)

Mà \(x^2+4\ge0+4=4\Rightarrow x^2+4\in\left\{4;8\right\}\)

\(\Rightarrow x^2\in\left\{0;4\right\}\)

\(\Rightarrow x\in\left\{-2;0;2\right\}\)

Với \(x=-2\Rightarrow\frac{x+2}{x^2+4}=\frac{0}{4+4}=0\in Z\left(TM\right)\)

Với \(x=0\Rightarrow\frac{x+2}{x^2+4}=\frac{2}{0+4}=\frac{1}{2}\notin Z\left(0TM\right)\)

Với \(x=2\Rightarrow\frac{x+2}{x^2+4}=\frac{4}{4+4}=\frac{1}{2}\notin Z\left(0TM\right)\)

Do đó \(x=-2\)

Vậy ...

1/ 0, 71

2/ Tương tự 2 câu 1, 3 nhé!

3/ 11,25

Tick đúng nha! Thanks!