Một hình thang vuông ABCD có đường cao A D = π , đáy nhỏ A B = π , đáy lớn C D = 2 π . Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng:
A. 4 3 π 4
B. 7 3 π 4
C. 10 3 π 4
D. 13 3 π 4
Một hình thang vuông ABCD có đường cao A D = π đáy nhỏ A B = π đáy lớn C D = 2 π Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng:
A. 4 3 π 4
B. 7 3 π 4
C. 10 3 π 4
D. 13 3 π 4
Đáp án A
Lấy I là trung điểm CD. Thể tích vật tròn xoay là
π . π . π 2 + 1 3 π . π . π 2 = 4 3 π 4
Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a 3 là:
A. 2 π a 2 3 B. 2 π a 2
C. π a 2 D. π a 2 3
Chọn A.
Hình trụ có bán kính đáy a và đường cao a 3 nên:
S xq = 2 π rh = 2 π a.a 3 = 2 π a 2 3
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:
A. 2 π a 3 B. 2 π a 3 /3
C. 4 π a 3 D. π a 3
Chọn A.
Thiết diện qua trục của hình trụ là hình vuông nê hình trụ có bán kính đáy là a, chiều cao là 2a.
Do đó thể tích khối trụ là:
V = πR 2 h = 2 πa 3
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Chọn C.
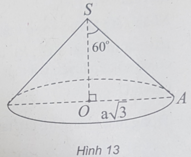
(h.13) Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết, đường tròn đáy có bán kính R = OA = a 3 và ∠ = 60 °
Trong tam giác SOA vuông tại O, ta có: OA = SO.tan60 ° ⇒ SO = a.
Do đó chiều cao của hình nón là h = a.
Vậy thể tích hình nón là: V = π a 3
Một khối trụ có chu vi đáy bằng 6 π cm và thiết diện đi qua là một hình chữ nhật có độ dài đường chéo bằng 10 cm. Thể tích khối trụ là:
A. 72 π ( cm 3 ) B. 24 π ( cm 3 )
C. 48 π ( cm 3 ) D. 18 π 34 ( cm 3 )
Chọn A.
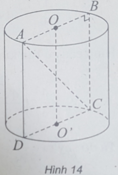
(h.14) Gọi O, O' là hai tâm của hai đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6 π (cm) nên bán kính đáy của hình trụ là: R = 3 (cm)
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 (cm) và AB = 2R = 6 (cm) nên chiều cao của hình trụ là:
h = OO' = BC = 8 (cm)
Vậy thể tích khối trụ là: V = π R 2 h = 72 π ( cm 3 )
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:
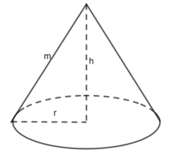
A. π . r 2 h ( c m 3 ) B. (1/3) π . r 2 h ( c m 3 )
C. π .r.m ( c m 3 ) D. π r(r+m) ( c m 3 )
Thể tích hình nón : V = (1/3) π . r 2 h ( c m 3 )
Vậy chọn đáp án B
Sử dụng các thông tin và hình bên để trả lời các câu hỏi sau:
Một đồ chơi “ lắc lư” của trẻ em gồm một hình nón gắn với nửa hình cầu (chiều cao của hình nón bằng đường kính của đường tròn đáy).Có hai loại đồ chơi: loại thứ nhất cao 9cm ,loại thứ hai cao 18cm
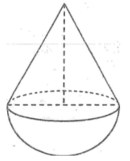
Trong các số sau đây:
A.30 π ( c m 3 ) B. 36 π ( c m 3 )
C. 72 π ( c m 3 ) D.610 ( c m 3 )
Số nào là thể tích của đồ chơi loại thứ nhất?
Thể tích đồ chơi loại thứ nhất là 36 π ( c m 3 )
Vậy chọn đáp án B
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Cho hình trụ có bán kính đáy a và có thiết diện qua trục là một hình vuông. Diện tích xung quanh của hình trụ là:
A. 3π a 2 B. 2π a 2
C. 4π a 2 D. π a 2
Chọn C.
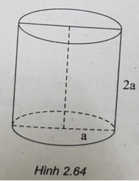
(h.2.63) Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông nên chiều cao hình trụ bằng 2a.
Vậy diện tích xung quanh khối trụ là:
S xq = 2 πRh = 4 πa 2