Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=2x (trong đó a là hằng số và x thay đổi thuộc khoảng 0 ; a 3 2 ). Tính thể tích lớn nhất V m a x của hình chóp S.ABC
A. V m a x = a 3 6
B. V m a x = a 3 2 4
C. V m a x = a 3 8
D. V m a x = a 3 2 12
Những câu hỏi liên quan
Cho hình chóp S.ABC có SASBSCABACa, BC2x (trong đó a là hằng số và x thay đổi thuộc khoảng
0
;
a
3
2
. Tính thể tích lớn nhất Vmax của hình chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=2x (trong đó a là hằng số và x thay đổi thuộc khoảng 0 ; a 3 2 . Tính thể tích lớn nhất Vmax của hình chóp S.ABC
có nge9ejr 0 uiwu3433r2///3
Cho hình chóp S.ABC có SASBSCABACa, BCa
2
. Số đo góc giữa hai đường thẳng AB và SC bằng ? A.
90
o
B.
60
o
C.
45
o
D.
30
o
Đọc tiếp
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=a 2 . Số đo góc giữa hai đường thẳng AB và SC bằng ?
A. 90 o
B. 60 o
C. 45 o
D. 30 o
Đáp án là B
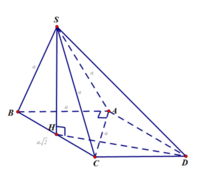
Cách 1. Xác định và tính góc giữa hai đường thẳng.
Tam giác ABC vuông tại A
Do SA=SB=SC nên nếu gọi H là hình chiếu vuông góc của S lên (ABC) thì H là tâm đường tròn ngoại tiếp tam giác ABC mà tam giác ABC vuông tại A nên H là trung điểm của BC.
Dựng hình bình hành ABCD. Khi đó:(AB,SC)=(CD,SC) và CD=AB=a. Tam giác SBC vuông tại S
có SH là đường trùng tuyến nên SH= a 2 2
Tam giác CDH có
theo định lý Cô- Sin ta có
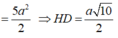
Tam giác SHD vuông tại H nên
Tam giác SCD có:
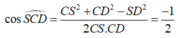
Cách 2. (Hay phù hợp với bài này) Ứng dụng tích vô hướng.
Theo giả thiết có
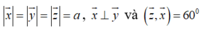
Ta có
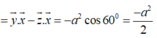
Suy ra:
Đúng 0
Bình luận (0)
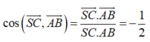
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a, BC = a 2 . Số đo góc giữa hai đường thẳng AB và SC bằng
A. 900.
B. 600.
C. 450.
D. 300.
Chọn B.
Cách 1. Xác định và tính góc giữa hai đường thẳng
∆
ABC vuông tại A 
Do SA = SB = SC nên nếu gọi H là hình chiếu vuông góc của S lên (ABC) thì H là tâm đường trong ngoại tiếp tam giác ABC mà ∆ ABC vuông tại A nên H là trung điểm của BC. Dựng hình bình hành ABCD. Khi đó (AB;SC) = (CD;SC) và CD = AB = a
∆
SBC vuông tại S (vì 
có SH là đường trung tuyến nên SH =
a
2
2
theo định lí Cô – Sin ta có
∆ SHD vuông tại H nên
∆
SCD có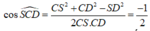 
Cách 2. (Hay phù hợp với bài này) Ứng dụng tích vô hướng
Đặt 
Theo giả thiết ta có: 
Ta có: 
Xét 
Suy ra: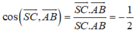 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a và BC=a 2 (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AB và SC là
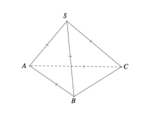
A. 45°.
B. 60°.
C. 90°.
D. 30°.
Cho hình chóp S.ABC, lấy các điểm A, B, C lần lượt thuộc các tia SA, SB, SC sao cho SA aSA, SB bSB ,SC cSC, trong đó a, b, c là các số thay đổi. Tìm mối liên hệ giữa a, b ,c để mặt phẳng (ABC) đi qua trọng tâm tam giác ABC ? A. a + b +c 3 B. a + b +c 4 C. a + b +c 2 D. a + b +c 1
Đọc tiếp
Cho hình chóp S.ABC, lấy các điểm A', B', C' lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA', SB = bSB' ,SC = cSC', trong đó a, b, c là các số thay đổi. Tìm mối liên hệ giữa a, b ,c để mặt phẳng (A'B'C') đi qua trọng tâm tam giác ABC ?
A. a + b +c =3
B. a + b +c =4
C. a + b +c =2
D. a + b +c =1
Đáp án A.
Hướng dẫn giải:
Nếu a = b = c = 1 thì SA = SA',SB = SB',SC = SC'
nên ( A B C ) ≡ ( A ' B ' C ' )
Dễ thấy (A'B'C') đi qua trọng tâm của tam giác ABC
⇒ a + b + c = 3 là đáp án đúng
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC có SA = SB = SC = AB = AC = a và B C = a 2 . Tính góc giữa hai vectơ A B → v à S C → .
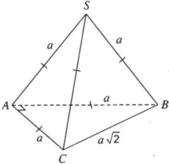
Ta tính côsin của góc giữa hai vectơ S C → và A B → . Ta có
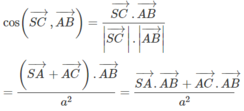
Theo giả thiết ta suy ra hình chóp có các tam giác đều là SAB, SAC và các tam giác vuông là ABC vuông tại A và SBC vuông tại S.
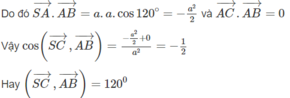
Vậy góc giữa hai vectơ A B → v à S C → bằng 120 o .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC= a 2 . Tính số đo của góc (AB;SC) ta được kết quả
A. 90 °
B. 30 °
C. 60 °
D. 45 °
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, B C = a 2 . Tính số đo của góc giữa hai đường thẳng AB và SC ta được kết quả
A. 90 °
B. 30 °
C. 60 °
D. 45 °
Chọn C
* Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABC), theo đầu bài SA=SB=SC và tam giác ABC vuông cân tại A ta có H là trung điểm của BC. Gọi M, N lần lượt là trung điểm của SA, SB ta có:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có ABBCCAa, SASBSCa
3
M là điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng
Đọc tiếp
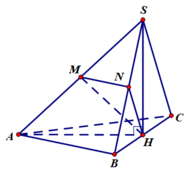
Cho hình chóp S.ABC có AB=BC=CA=a, SA=SB=SC=a 3 M là điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng
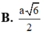
