Giá trị cực đại của hàm số y = x + sin2x trên 0 ; π là:
A. π 6 + 3 2
B. 2 π 3 + 3 2
C. 2 π 3 - 3 2
D. π 3 + 3 2
Giá trị cực đại của hàm số y = x + sin 2 x trên 0 ; π là:
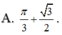
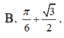
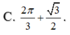
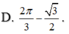
Xét tính đúng sai của các mệnh đề sau (với a, b, c, d là các hằng số).
(I): Giá trị cực đại của hàm số y = f x luôn lớn hơn giá trị cực tiểu của nó.
(II): Hàm số y = a 4 + b x + c a ≠ 0 luôn có ít nhất một cực trị
(III): Giá trị cực đại của hàm số y = f x luôn lớn hơn mọi giá trị của hàm số đó trên tập xác định.
(IV): Hàm số y = a x + b c x + d c ≠ 0 ; a d − b c ≠ 0 không có cực trị.
Số mệnh đề đúng là:
A. 1
B. 4
C. 3
D. 2
Đáp án là D.
Ta thấy (II) và (IV) là mệnh đề đúng.
Tìm điểm cực đại của hàm số y = s i n 2 x + 3 c o s x + 1 với x ∈ (0; π)
A. x = 0
B. x = π
C. x = π 6
D. x = π 3
Biết rằng hàm số y = sin2x + b.cosx - x ( 0 < x < π ) đạt cực trị tại các điểm x = π 6 và x = π 2 Tính giá trị của biểu thức T = a - b
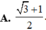
![]()
![]()
![]()
Biết rằng hàm số y = sin 2 x + b cos 2 x - x ( 0 < x < π ) đạt cực trị tại các điểm x = π 6 và x = π 2 Tính giá trị của biểu thức T = a-b
A. 3 + 1 2
B. 3 - 1 2
C. 3 - 1
D. 3 + 1
Đáp án là B.
Ta có y , = 2 a . cos 2 x - 2 b sin 2 x - 1 .Để hàm số đạt cực trị các điểm x = π 2 và x = π 2 thì y , ( π 6 ) = 0 y , ( π 2 ) = 0 ⇔ a - 3 b - 1 = 0 - 2 a - 1 = 0 ⇔ a = - 1 2 b = - 3 2 ⇒ a - b = 3 - 1 2
Tìm giá trị lớn nhất của hàm số y = x + sin 2 x trên đoạn [ 0 ; π ]
A. π
B. 0
C. 3 π 4 + 1 2
D. 3 π 4
Đáp án là A.
Ta có: y , = 1 + 2 sin x cos x = 1 + sin 2 x
y , = 0 ⇔ x = - π 4 + k π , k ∈ ℤ
Vì x ∈ 0 ; π nên x = 3 π 4
Tính được: y ( 0 ) = 0 ; y ( π ) = π ; y ( 3 π 4 ) = 3 π 4 + 1 2
Vậy: m a x [ 0 ; π ] y = y ( π ) = π .
Giá trị cực đại của hàm số y = 2 x + cos 2 x trên 0 ; π 4 là
A. y min = π 4 ; y max = 1
B. y min = π 2 8 − 2 2 ; y max = π 4
C. y min = 1 ; y max = π 2 8 + 2 2
D. y min = π 2 8 ; y max = π 2 8 + 2 2
Trên đoạn - π 3 ; 4 π , hàm số y = x - sin 2 x + 3 có mấy điểm cực đại?
A. 2
B. 3
C. 4
D. 5
Cho hàm số y=f(x) có đạo hàm xác định trên tập R / - 1 và đồ thị hàm số y=f(x) như hình vẽ. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số y=f(sin2x) trên 0 ; π 2 . Tính P=m.M
A. P=0
B. P=8
C. P=12
D. P=4